No estudo de Conjuntos, trabalhamos com alguns conceitos primitivos, que devem ser entendidos e aceitos sem definição. Para um estudo mais aprofundado sobre a Teoria dos Conjuntos, pode-se ler: Naive Set Theory, Paul Halmos ou Axiomatic Set Theory, P. Suppes. O primeiro deles foi traduzido para o português sob o título (nada ingênuo de): Teoria Ingênua dos Conjuntos.

• Conjunto
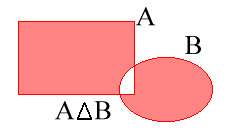
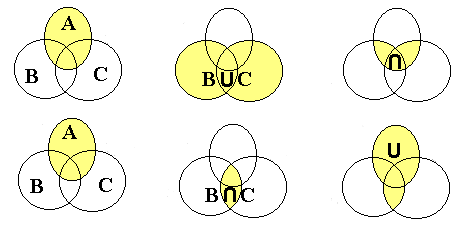  • O conjunto de todos os brasileiros
  • O conjunto de todos os números naturais (N)
  • O conjunto de todos os números reais tal que x²-4=0

  Em geral, um conjunto é denotado por uma letra maiúscula do alfabeto: A,B,C,...,Z.

• Elemento
  • José da Silva é um elemento do conjunto dos brasileiros.
  • 1 é um elemento do conjunto dos números naturais.
  • -1/3 é um elemento do conjunto dos números reais que satisfaz à equação x ² - 4 = 0.

  Em geral, um elemento de um conjunto, é denotado por uma letra minúscula do alfabeto: a,b,c,...,z.

• Pertinência
  • José da Silva pertence ao conjunto dos brasileiros.
  • 1 pertence ao conjunto dos números naturais.
  • -1/3 pertence ao conjunto de números reais que satisfaz à equação x ² - 4 = 0.

  Se um elemento pertence a um conjunto utilizamos o símbolo: , que se lê: "pertence". Para afirmar que 1 é um número natural, escrevemos:

  

  Para afirmar que 0 não é um número natural, escrevemos:

  

  Um símbolo matemático para a negação é a barra /.

Um conjunto é denotado, muitas vezes com elementos dentro de duas chaves { e }, através de duas formas básicas e de uma forma geométrica:

• Apresentação

  Os elementos do conjunto estão dentro de duas chaves { e }.

  • A = { a, e, i, o, u }
  • N = { 1, 2, 3, 4, ... }
  • M = { João, Maria, José }

• Propriedade

  O conjunto é descrito por uma ou mais propriedades.

  • A = { x : x é uma vogal}
  • N = { x : x é um número natural}
  • M = { x : x é uma pessoa da família de Maria}

• Diagrama de Venn-Euler (lê-se: "Ven-óiler")

  Os conjuntos são mostrados graficamente.

  

Dados os conjuntos A e B, diz-se que A está contido em B, denotado por , se todos os elementos de A também estão em B. Algumas vezes diremos que um conjunto A está propriamente contido em B, quando o conjunto B, além de conter os elementos de A, contém também outros elementos. O conjunto A é denominado subconjunto de B e o conjunto B é o superconjunto que contém A.

• Conjunto vazio
  Conjunto que não tem elementos. É representado por { } ou por Ø. O conjunto vazio está contido em todos os conjuntos.

• Conjunto universo
  É o conjunto que contém todos os elementos do contexto no qual estamos trabalhando. O conjunto universo é representado por uma letra U.
  Dado um conjunto de n elementos, temos exatamente 2ⁿ subconjuntos, incluidos estes dois especiais.
  O conjunto dos suconjuntos de C é denominado "Partes" de C e escrevemos P(C)
  Ex.: C = {a,b,c}, n = 3, temos 2³ = 8 elementos.
  P(C) = {{},{1},{2},{3},{1,2},{1,3},{2,3}, {1,2,3}}

A reunião dos conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A ou ao conjunto B.

A interseção dos conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A e ao conjunto B.

Quando a interseção de dois conjuntos A e B é o conjunto vazio, dizemos que estes conjuntos são disjuntos.

• Fechamento
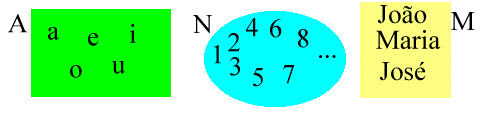
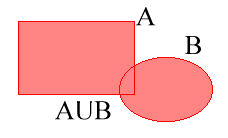
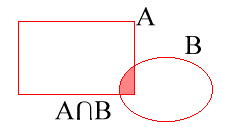
  Quaisquer que sejam os conjuntos A e B, então a reunião de A e B, denotada por A U B e a interseção de A e B, denotada por AB, ainda são conjuntos no universo.

• Reflexiva
  Qualquer que seja o conjunto A, tem-se que:
  A U A = A
  A A = A

• Inclusão
  Quaisquer que sejam os conjuntos A e B, tem-se que:
  A A U B, B A U B
  A B A , A B B
  

• Inclusão relacionada
  Quaisquer que sejam os conjuntos A e B, tem-se que:
  AB <=> AUB=B
  AB <=> AB=A

• Associativa
  Quaisquer que sejam os conjuntos A, B e C, tem-se que:
  A U ( B U C ) = ( A U B ) U C ==>podemos esccrever: A U B U C
  A(B C) = (AB)C ==>podemos esccrever: AB C

• Comutativa
  Quaisquer que sejam os conjuntos A e B, tem-se que:
  AUB=BUA
  AB=BA

• Elemento neutro para a reunião
  O conjunto vazio Ø é o elemento neutro para a reunião de conjuntos, tal que para todo conjunto A, se tem:
  A U Ø=A

• Elemento "nulo" para a interseção
  Se tomarmos a interseção do conjunto vazio Ø com qualquer outro conjunto A, teremos o próprio conjunto vazio.
  AØ=Ø

• Elemento neutro para a interseção
  O conjunto universo U é o elemento neutro para a interseção de conjuntos, tal que para todo conjunto A, se tem:
  A U = A

• Distributiva
  Quaisquer que sejam os conjuntos A, B e C, tem-se que:
  A ( B U C ) = ( A B ) U ( A C )
  A U ( B C ) = ( A U B ) (A U C )
  

  ---

  Diferença de conjuntos

  A diferença entre os conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.

  
  

  ---

  Complemento (ou Complementar) de um conjunto

  O complemento do conjunto B contido no conjunto A, denotado por C B_A, é a diferença entre os conjuntos A e B, ou seja, é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.

  Quando não existe dúvida sobre o universo U em que trabalhamos, simplesmente utilizamos a letra c colocada como um expoente no conjunto, para indicar o complemento deste conjunto.

  
  

  Alguns exemplos especiais são:

  

  ---

  Leis de Augustus De Morgan

  O complementar da reunião de conjuntos é a interseção dos complementares desses conjuntos.

  

  O complementar da interseção de conjuntos é a reunião dos complementares desses conjuntos.

  

  ---

  Diferença simétrica

  A diferença simétrica entre os conjuntos A e B é o conjunto de todos os elementos que pertencem à reunião dos conjuntos A e B e não pertencem à interseção dos conjuntos A e B.

  
  

  Exercício: A partir de conjuntos A, B e C, mostrar que:

  1. A=Ø se, e somente se, B é a diferença simétrica entre A e B.
  2. Com base no ítem anterior, concluir que o conjunto vazio é o elemento neutro para a operação de diferença simétrica.
  3. A diferença simétrica é comutativa.
  4. A diferença simétrica é associativa.
  5. A diferença simétrica entre A e A é o conjunto vazio.
  6. A interseção entre A e a diferença simétrica de B e C é distributiva, isto é:
  7. A diferença simétrica entre A e B está propriamente contida na reunião das diferenças simétricas de A e C e de B e C, isto é: