Cabri

FAMILIARIZANDO-SE COM O PROGRAMA CABRI GEOMETRY

obs: para indicar menus a serem selecionados, vamos considerar a barra
de menus numerada de 1 à 11. Na figura temos selecionado Menu 3 / Polígono

Quando falamos em instrumentos de construção em Geometria pensamos logo em régua e compasso. Cabri-Geometry é um programa de construção que nos oferece "régua e compasso eletrônicos", sendo a interface de menus de construção em linguagem clássica da Geometria.

Os desenhos de objetos geométricos são feitos a partir das propriedades que os definem. Mas não é só isto que ele nos oferece, e aqui está a riqueza do software: através de deslocamentos aplicados aos elementos que compõe o desenho, este se transforma, mantendo as relações geométricas que caracterizam a situação.

Assim, para um dado objeto temos associada uma coleção de "desenhos em movimento", e as características invariantes qua aí aparecem correspondem as propriedades geométricas do objeto. Do ponto de vista de construção de conhecimento o que significa este recurso? Muito! Vejamos:

se, sob ação de movimento, o desenho não corresponde ao que queremos duas são as possibilidades: ou o objeto foi mal construído (isto é, as propriedades que caracterizam o objeto não foram bem utilizadas), ou nossa imagem visual do objeto é que não é adequada (isto é, a construção foi feita corretamente, mas nossa visualização é que está mal). Em qualquer um dos casos, o recurso do "desenho em movimento" leva ao ajuste entre componente conceitual e componente visual do objeto.
configurações clássicas passam a ter múltiplos aspectos visuais, e com isto passam a ser identificadas em situações não prototípicas.
os "desenhos em movimento" criam naturalmente um ambiente de investigação; os invariantes se destacam e isto nos intriga.

Para ter uma idéia dos movimentos das figuras construídas no Cabry-Geometry, visite aqui uma página em java.

Nosso primeiro trabalho no curso é de familiarização com o programa Cabri-Geometry. Para isso:

explore os recursos do programa. Consulte o manual somente quando tiver muita dificuldade para avançar na exploração. Lembre-se que o programa tem um "help" que fica a disposição com a tecla F1.

construa as figuras geométricas abaixo; procure diferentes estratégias para a mesma figura. Mas antes alguns comentários:

menus a serem utilizados: 1 à 5 e Menu 11 / Esconder/Mostrar (este para 'esconder' objetos que não interessam no desenho final)
Atenção: As figuras devem ser estáveis sob a ação de movimento. Isto é: ao mover-se os vértices livres, elas devem manter as mesmas propriedades: o quadrado permenece quadrado; o paralelogramo permanece paralelogramo; etc...
(para isso selecione o 'pointer' e aproxime o cursor dos elementos móveis da figura construída. Mantenha o botão da esquerda do mouse clicado e arraste o vértice da figura)
Algumas das figuras podem ser obtidas diretamente como polígonos regulares. Não use esse recurso. Você deve fazer a construção da figura!
Feita as construções, grave como arquivo .fig.

APRENDENDO A FAZER MACROS

Abaixo, temos uma possível construção para triângulo equilátero:

marcar dois pontos A e B e traçar o segmento AB;
traçar os círculos de centro A e B raio AB. Marcar um dos pontos de intersecção dos dois círculos, que vamos chamar de C;
traçar os segmentos AC e BC;
'esconder' os círculos para que apareça somente o triângulo. Para isso selecione Menu 11 / Esconder/Mostrar e com o cursor selecione os círculos.

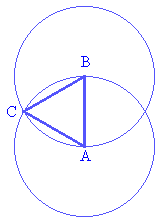Nessa construção os únicos objetos móveis são os pontos A e B, e ao mover-se esses pontos o triângulo muda de tamanho mas permanece sempre equilátero.

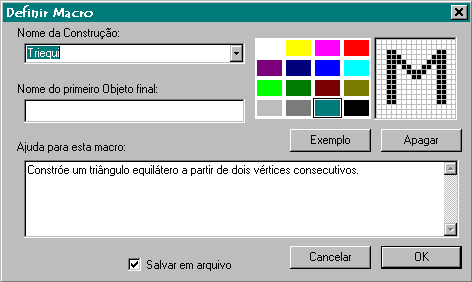
Podemos gravar esse procedimento na forma de macro. Com isso, se temos dois pontos A e B e ativamos o macro, obtemos imediatamente o triângulo equilátero de lado AB! Vejamos como fazer isso:

selecionar Menu 7 / Objetos Iniciais; com o cursor marcar os pontos A e B (após a seleção os pontos devem ficar 'piscando')
selecionar Menu 7 / Objetos Finais; com o cursor marcar os lados AB, BC e CA (após a seleção os segmentos ficam pontilhados)
selecionar Menu 7 / Definir Macro
informar o nome do macro e escrever instruções de construção:
selecionar ok. Seguir os procedimentos para salvar no seu disquete; não esqueça que a terminação deve ser .mac.
para ativar o macro: selecionar Arquivo / Novo ; marcar dois pontos A e B; selecionar Menu 7 / Triequi ( nome atribuído ao macro); com o cursor indicar os pontos A e B ; tem-se de imediato a construção do triângulo equilátero com vértices A e B.