Algarismos significativos
Incertezas nas medidas
Por
Milton Procópio de Borba
Um exemplo:
Um certo comprimento y (em cm) foi medido 40 vezes:
|
72,55 |
73,27 |
73,17 |
73,07 |
74,57 |
71,07 |
72,88 |
73,19 |
73,24 |
72,94 |
|
72,60 |
73,94 |
73,85 |
75,01 |
73,53 |
71,98 |
74,70 |
75,59 |
76,22 |
74,14 |
|
74,40 |
73,35 |
75,11 |
74,01 |
73,41 |
76,30 |
73,65 |
73,54 |
73,62 |
70,58 |
|
74,75 |
72,65 |
72,29 |
72,15 |
73,81 |
74,47 |
72,44 |
74,99 |
74,11 |
74,30 |
A média calculada é de Y = 73,64 cm, com um desvio padrão de s = 1,2 m.
Veremos AGORA, que os algarismos das centenas não são significativos.
Realmente, vamos
calcular a probabilidade de Y ser 73,60 cm, 73,61
cm, 73,62 cm, 73,63 cm, ..., 73,68
cm ou 73,69 cm.
A probabilidade
de Y, com 4 algarismos, ser 73,60 cm:
P(73,595 , 73,605) =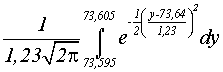 
= 0,00324171 (9,998%)
A probabilidade de Y ser 73,61 cm:
P(73,605 , 73,615) =
0,00324246 (10,000%)
A probabilidade de Y ser 73,62 cm:
P(73,615 , 73,625) =
0,00324300 (10,001%)
A probabilidade de Y ser 73,63 cm:
P(73,625 , 73,635) =
0,00324332 (10,002%)
A probabilidade de Y ser 73,64 cm:
P(73,635 , 73,645) =
0,00324342 (10,003%)
A probabilidade de Y ser 73,65 cm:
P(73,645 , 73,655) =
0,00324332 (10,002%)
A probabilidade de Y ser 73,66 cm:
P(73,655 , 73,665) =
0,00324300 (10,001%)
A probabilidade de Y ser 73,67 cm:
P(73,665 , 73,675) =
0,00324246 (10,000%)
A probabilidade de Y ser 73,68 cm:
P(73,675 , 73,685) =
0,00324171 (9,998%)
A probabilidade de Y ser 73,69 cm:
P(73,685 , 73,695) =
0,00324074 (9,995%)
Todas as probabilidades são praticamente iguais, ou seja, qualquer algarismo entre 0 e 9 têm quase a mesma chance de ser o 4o algarismo desta
medida.
O mesmo não acontece, neste mesmo nível, com o 3o algarismo:
Realmente, vamos
calcular a probabilidade de Y ser 73,0 cm, 73,1
cm, 73,2 cm, 73,3 cm, ..., 73,8
cm ou 73,9 cm.
A probabilidade
de Y, com 3 algarismos, ser 73,0 cm:
P(72,95 ,
73,05) =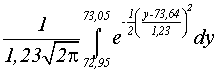 
= 0,02832 (9,1%)
A probabilidade de Y
ser 73,1 cm: P(73,05
, 73,15) = 0,02945 (9,4%)
A probabilidade de Y
ser 73,2 cm: P(73,15
, 73,25) = 0,03042 (9,7%)
A probabilidade de Y
ser 73,3 cm: P(73,25
, 73,35) = 0,03121 (10,0%)
A probabilidade de Y
ser 73,4 cm: P(73,35
, 73,45) = 0,03181 (10,2%)
A probabilidade de Y
ser 73,5 cm: P(73,45
, 73,55) = 0,03222 (10,3%)
A probabilidade de Y
ser 73,6 cm: P(73,55
, 73,65) = 0,03241 (10,4%)
A probabilidade de Y
ser 73,7 cm: P(73,65
, 73,75) = 0,03239 (10,4%)
A probabilidade de Y
ser 73,8 cm: P(73,75
, 73,85) = 0,03215 (10,3%)
A probabilidade de Y
ser 73,9 cm: P(73,85
, 73,95) = 0,03171 (10,2%)
Note que a maior probabilidade é a do algarismo 6.
Maior certeza, temos no 2o algarismo:
A probabilidade
de Y, com 2 algarismos, ser 70 cm:
P(69,5 , 70,5)
= 
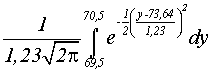= 0,00496 (0,5%)
A probabilidade de Y
ser 71 cm: P(70,5
, 71,5) = 0,0356 (3,6%)
A probabilidade de Y
ser 72 cm: P(71,5
, 72,5) = 0,136 (13,6%)
A probabilidade de Y
ser 73 cm: P(72,5
, 73,5) = 0,278 (27,8%)
A probabilidade de Y
ser 74 cm: P(73,5
, 74,5) = 0,303 (30,3%)
A probabilidade de Y
ser 75 cm: P(74,5
, 75,5) = 0,177 (17,7%)
A probabilidade de Y
ser 76 cm: P(75,5
, 76,5) = 0,0552 (5,5%)
A probabilidade de Y
ser 77 cm: P(76,5
, 77,5) = 0,0092 (0,9%)
A probabilidade de Y
ser 78 cm: P(77,5
, 78,5) = 0,0008 (0,1%)
A probabilidade de Y
ser 79 cm: P(78,5
, 79,5) = 0,00004 (0,0%)
Note que a maior probabilidade é a do algarismo 4.
Então, representamos: y = (73,6 ± 1,2 ) cm, significando que provavelmente
(73,6 - 1,2) cm <
y < (73,6 + 1,2) cm.
Mais especificamente, VEREMOS que
|
72,4 cm |
< y < |
74,8 cm |
, com 68,3 |
% de chance |
|
72,8 cm |
< y < |
74,4 cm |
, com 50,0 |
% de chance |
|
71,2 cm |
< y < |
76,0 cm |
, com 95,4 |
% de chance |
|
70,0 cm |
< y < |
77,2 cm |
, com 99,7 |
% de chance (quase 100%). |
Realmente: 72,4 e 74,8 estão 1,2 distante da média 73,6,
ou seja, um desvio padrão.
= 
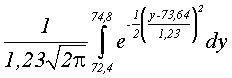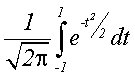= 0,683
Analogamente: 70,0 e 77,2 estão 3,6 distante da média 73,4, ou seja, três desvio padrões
= 
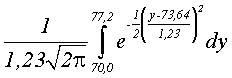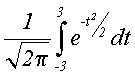= 0,997
Estes são os seguintes convencionados níveis de erro/incerteza:
|
Incerteza |
Símbolo |
Intervalo |
Confiança |
|
Erro padrão |
s |
Y - s <
y < Y + s |
68,27% |
|
Erro provável |
D = 0,6745 s |
Y - D <
y < Y + D |
50% |
|
|
2 s |
Y - 2s <
y < Y + 2s |
95,4% |
|
Erro limite estatístico |
3 s |
Y - 3s <
y < Y + 3s |
99,73% |
|
Erro limite |
L |
Y - L
< y <
Y + L |
100% |