 |
Quando construímos uma tabela de freqüências para uma variável quantitativa utilizando agrupamento de valores em classes, estamos resumindo a informação contida nos dados. Isto é desejável quando o número de dados é grande e sem um algum tipo de resumo ficaria difícil tirar conclusões sobre o comportamento da variável em estudo.
Porém, quando a quantidade de dados disponíveis não é tão grande, o resumo promovido pelo histograma não é aconselhável.
Para os casos em que o número de dados é pequeno, uma alternativa para a visualização da distribuição desses dados são os gráficos denominados diagrama de pontos e diagrama de ramo-e-folhas.
O Diagrama de Pontos
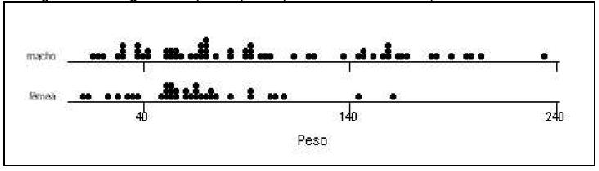
Uma representação alternativa ao histograma para a distribuição de freqüências de uma variável quantitativa é o diagrama de pontos, como aqueles mostrado mostrados na Figura 16.
Neste gráfico, cada ponto representa uma observação com determinado valor da variável. Observações com mesmo valor são representadas com pontos empilhados neste valor.
Através da comparação dos diagramas de pontos da Figura 16, podemos ver que os ursos machos possuem pesos menos homogêneos (mais dispersos) do que as fêmeas, que estão concentradas na parte esquerda do eixo de valores de peso.
O Diagrama de Ramo-e-Folhas
Outro gráfico útil e simples para representar a distribuição de freqüências de uma variável quantitativa com poucas observações é o diagrama de ramo-e-folhas. A sua sobre os demais é que ele explicita os valores dos dados, como veremos.
Exemplo dos ursos marrons (continuação):
Dos 35
ursos fêmeas observados, somente 20 puderam ter sua idade estimada. Para
visualizar a distribuição dos valores de idade dessas fêmeas, usaremos um
diagrama de ramo-efolhas, já que um histograma resumiria mais ainda algo que já
está resumido.
Os 20 valores de idade (em meses) disponíveis, já ordenados são:
8 9 11 17 17 19 20 44 45 53 57 57 57 58 70 81 82 83 100 104
Podemos organizar os dados, separando-os pela dezenas, uma em cada linha:
8 9 11 17 17 19 20 44 45 53 57 57 57 58 70 81 82 83 100 104
Como muitos valores em cada linha tem as dezenas em comum, podemos colocar as dezenas em evidência , separando-as das unidades por um traço. Ao dispor os dados dessa maneira, estamos construindo um diagrama de ramo-e-folhas (Figura 17). O lado com as dezenas é chamado de ramo, no qual estão dependuradas as unidades, chamadas folhas.
Os ramos e as folhas podem representar quaisquer unidades de grandeza (dezenas e unidades, centenas e dezenas, milhares e centenas, etc). Para sabermos o que está sendo representado, um ramo-e-folhas deve ter sempre uma legenda, indicando o que significam os ramos e as folhas.
Se a idade estivesse medida em dias, por exemplo, usando esse mesmo ramo-efolhas, poderíamos estabelecer que o ramo representaria as centenas e as folhas, as dezenas. Assim, 0|8 seria igual a 80 dias e 10|4 seria igual a 1040 dias.
Analisando o ramo-e-folhas para a idade dos ursos fêmeas, percebemos a existência de três grupos: fêmeas mais jovens (até 20 meses), fêmeas mais crescidas (de 44 a 58 meses) e um grupo mais velho (mais de 70 meses), com destaque para duas fêmeas bem mais velhas.
O ramo-e-folhas também pode ser usado para comparar duas distribuições de valores, como mostra a Figura 18. Aproveitando o mesmo ramo do diagrama das fêmeas, podemos fazer o diagrama dos machos, utilizando o lado esquerdo. Observe que as folhas dos ursos machos são dependuradas de modo espelhado, assim como explica a legenda, que agora deve ser dupla.
Observando a Figura 18, notamos que os ursos machos são, em geral, mais jovens do que os ursos fêmeas, embora possuam dois ursos bem idosos em comparação com os demais.
Importante: No ramo-e-folhas, estamos trabalhando, implicitamente, com freqüências absolutas. Assim, ao comparar dois grupos de tamanhos diferentes, devemos levar isso em conta. Caso os tamanhos dos grupos sejam muito diferentes, não se deve adotar o ramo-e-folhas como gráfico para comparação de distribuições.