Sistemas de Amortização e Empréstimos
Empréstimos
Em termos financeiros, a dívida
surge quando uma certa importância é emprestada por um certo prazo de tempo.
Quem assume a dívida obriga-se a pagá-la da seguinte forma: o valor tomado
emprestado mais os juros devidos, no prazo estipulado no acordo inicial.
Os empréstimos classificam-se em:
Curto e médio prazos:
caracterizam-se por serem saldados até 3 anos.
Longo prazo: sofrem
um tratamento especial por existir várias modalidades de restituição do
principal e dos juros. Tais empréstimos têm suas condições previamente
estipuladas por contrato entre as partes, ou seja, entre o credor e o devedor.
Amortização
Conceito: Ato de pagar as prestações que foram geradas
mediante tomada de empréstimo.
Período de amortização: é o
intervalo de tempo existente entre duas amortizações sucessivas.
Prazo de amortização: é o
intervalo de tempo, durante o qual são pagas as amortizações.
Parcelas de amortização:
corresponde às parcelas de devolução do principal, ou seja, do capital
emprestado
Nos sistemas de amortização os
juros serão sempre cobrados sobre o saldo devedor, considerando a taxa de juros
compostos, sendo que, se não houver pagamento de uma parcela, levará a um saldo
devedor maior, calculando juro sobre juro.
Saldo Devedor é o estado da dívida, ou seja,
o débito, em um determinado instante de tempo.
Sistemas
de Amortização
Definição: meios
pelos quais vai se pagando uma dívida contraída, de forma que seja escolhida
pelo devedor a maneira mais conveniente para ele.
Qualquer um dos sistemas de
amortização pode ter, ou não, prazo de carência.
Prazo de carência: período
compreendido entre o prazo de utilização e o pagamento da primeira amortização.
Durante esse prazo o devedor só paga os juros.
Veremos agora os principais
sistemas de amortização
Sistemas de Amortização Constante - SAC
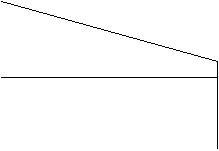
As parcelas de amortização são iguais entre si. Os juros são calculados, a cada período, multiplicando-se a taxa de juros contratada (na forma unitária) pelo saldo devedor existente no período anterior.
Por este sistema o credor exige a devolução do principal em n parcelas iguais, incidindo os juros sobre o saldo devedor.
Prestação Juro Amortização Períodos
![]()
![]()
![]()
![]()
![]()
![]()

![]()
C: 50.000
i: 1,5% a.m.
Amortizações mensais : 5
O principal foi emprestado no início do 1º mês e as
prestações e os juros serão pagos no fim de cada mês, ou seja, sempre sobre o
saldo devedor do período anterior. A amortização é mensal, a prestação é obtida
somando-se, ao final de cada período, a amortização com os juros.
50.000 = 10.000
5
|
Mês |
Saque |
Saldo devedor |
Amortização |
Juros |
Prestação |
|
0 |
50.000,00 |
50.000,00 |
- |
|
|
|
1 |
- |
40.000,00 |
10.000,00 |
750 |
10.750,00 |
|
2 |
- |
30.000,00 |
10.000,00 |
600 |
10.600,00 |
|
3 |
- |
20.000,00 |
10.000,00 |
450 |
10.450,00 |
|
4 |
- |
10.000,00 |
10.000,00 |
300 |
10.300,00 |
|
5 |
- |
- |
10.000,00 |
150 |
10.150,00 |
|
|
|
|
|
|
|
|
Total |
- |
- |
50.000,00 |
2.250,00 |
52.250,00 |
Sistema Francês- PRICE
Por este sistema o mutuário obriga-se a devolver o principal mais os juros em prestações iguais entre si. A dívida fica completamente saldada na última prestação.
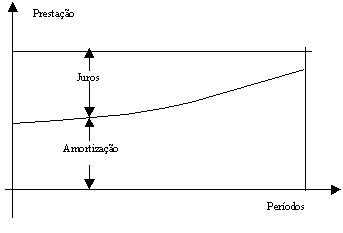
Precisamos calcular a prestação e separar a amortização dos
juros.
C: 50.000
i: 1,5%
a.m.
Amortizações mensais : 5
Calcular a prestação:
A = 50.000 =
50.000 ≈ 10.454,47
[P/A;1,5;5] 4,782645
Teremos então 5 prestações iguais de R$ 10.454,47. Os juros serão aplicados sobre o saldo devedor do período anterior, como no sistema de amortização constante.
A amortização será calculada pela diferença entre a prestação e o juro, e o saldo devedor será calculado como sendo a diferença entre o saldo devedor do período anterior e a amortização do período:
|
Mês |
Saque |
Saldo devedor |
Amortização |
Juros |
Prestação |
|
0 |
50.000,00 |
50000,00 |
- |
- |
- |
|
1 |
- |
40295,53 |
9704,47 |
750,00 |
10454,47 |
|
2 |
- |
30445,50 |
9850,03 |
604,43 |
10454,47 |
|
3 |
- |
20447,72 |
9997,78 |
456,68 |
10454,47 |
|
4 |
- |
10299,97 |
10147,75 |
306,72 |
10454,47 |
|
5 |
- |
0,00 |
10299,97 |
154,50 |
10454,47 |
|
|
|
|
|
|
|
|
Total |
- |
|
50.000,00 |
2272,33 |
52272,33 |
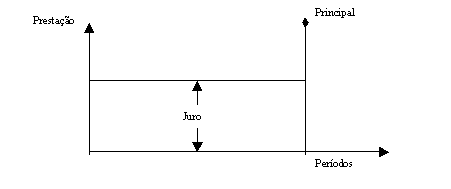
Sistema Americano
Após um certo prazo o devedor
paga, em uma única parcela, o capital emprestado, ou pode querer pagá-lo
durante a carência. A modalidade mais comum é aquela em que o devedor paga
juros durante a carência.
O devedor pode querer aplicar recursos
disponíveis e gerar um fundo que iguale o desembolso a ser efetuado para
amortizar o principal. Tal fundo é conhecido por “sinking fund” na
literatura americana e, na brasileira, por “fundo de amortização”.
C: 50.000
i: 1,5% a.m.
Amortização no 5º mês
Os juros são calculados sobre o saldo devedor, pagos no
final.
|
Mês |
Saque |
Saldo devedor |
Amortização |
Juros |
Prestação |
|
0 |
50.000,00 |
50.000,00 |
- |
- |
- |
|
1 |
- |
50.000,00 |
- |
750,00 |
750,00 |
|
2 |
- |
50.000,00 |
- |
750,00 |
750,00 |
|
3 |
- |
50.000,00 |
- |
750,00 |
750,00 |
|
4 |
- |
50.000,00 |
- |
750,00 |
750,00 |
|
5 |
- |
|
50.000,00 |
750,00 |
50.750,00 |
|
|
|
|
|
|
|
|
Total |
- |
|
50.000,00 |
3.750,00 |
53.750,00 |
Há capitalização dos juros durante a carência:
|
Mês |
Saque |
Saldo devedor |
Amortização |
Juros |
Prestação |
|
0 |
50.000,00 |
50.000,00 |
- |
- |
- |
|
1 |
- |
50.750,00 |
- |
750,00 |
|
|
2 |
- |
51.511,25 |
- |
761,25 |
|
|
3 |
- |
52.283,92 |
- |
772,67 |
|
|
4 |
- |
53.068,18 |
- |
784,26 |
|
|
5 |
- |
|
50.000,00 |
796,02 |
53.864,20 |
|
|
|
|
|
|
|
|
Total |
- |
|
50.000,00 |
3864,20 |
53.864,20 |
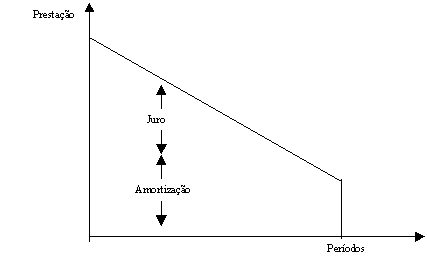
Sistema de amortizações variáveis
As parcelas de amortização são contratadas pelas partes e os juros são calculados sobre o saldo devedor.
Neste caso, a devolução do
principal (amortizações) é feita em parcelas desiguais. Isto pode ocorrer na
prática quando as partes fixam, antecipadamente, as parcelas de amortizações (sem
nenhum critério particular) e a taxa de juros cobrada.
Nestas condições a taxa de juros
também será sobre o saldo devedor. O empréstimo é amortizado mensalmente
conforme abaixo:.
1º mês –
10.000
2º mês –
15.000
3º mês –
10.000
4º mês –
15.000
C:
50.000
i: 1,5% a.m.
Amortização: 4 meses
Coloca-se inicialmente as
amortizações, a seguir são calculados os juros sobre o saldo devedor do período
anterior e calculada a prestação:
|
Mês |
Saque |
Saldo devedor |
Amortização |
Juros |
Prestação |
|
0 |
50.000,00 |
50.000,00 |
- |
- |
- |
|
1 |
- |
40.000,00 |
10.000,00 |
750,00 |
10.750,00 |
|
2 |
- |
25.000,00 |
15.000,00 |
600,00 |
15.600,00 |
|
3 |
- |
15.000,00 |
10.000,00 |
375,00 |
10.375,00 |
|
4 |
- |
0,00 |
15.000,00 |
225,00 |
15.225,00 |
|
5 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
Total |
- |
|
50.000,00 |
1.950,00 |
51.950,00 |
Bibliografia
MATHIAS, Washington Franco; GOMES, José Maria, Matemática
Financeira. São Paulo, Ed. Atlas,1989. 341-406 p.