Depreciação

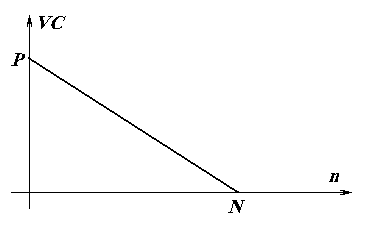
Contabilmente, depreciação é uma DESPESA equivalente à perda do valor de um bem, quer seja por deterioração, quer seja por obsolescência.

Na declaração anual de Imposto de Renda, a depreciação pode ser abatida das receitas.

Isto provoca um menor lucro contábil e conseqüentemente, menos imposto a pagar.  

Para evitar o lançamento de altos valores de depreciação, o governo estabelece regras definidas para cada tipo de bem (por exemplo: 25 anos para prédios, 10 anos para equipamentos, 5 anos para veículos, salvo justificativas adequadas de uma “maior” utilização).

Em todos os casos, a Depreciação Contábil considerada é Linear, isto é

A depreciação anual é constante (até o prazo N ), valendo

DC = (1/N ) . P

Aqui,  DC = Depreciação Contábil;

N = prazo de depreciação contábil;

1/N = fator de depreciação contábil;

P = Preço de compra.  

O Valor Contábil, depois de n anos é dado, então, por  

VC(n) = P – n . DC è VC(n) = P – (P/N) . n  

Graficamente, temos uma reta decrescendo de VC(0) = P até VC(N) = 0. 

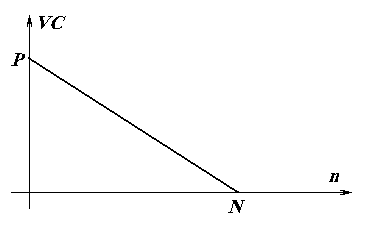
Podemos, ainda, considerar que com o passar dos anos, VC(n) forma uma
Progressão Aritmética (PA), com primeiro termo VC(0) = P e razão –P/N:  

VC(0) = P , P – P/N , P – 2.P/N , ..., VC(N) = P – N.P/N = 0  

A fim de fazer previsões e melhor planejar novos investimentos, se torna interessante conhecermos uma estimativa mais real para a depreciação e conhecer, por exemplo, o valor de venda deste bem.  

Costuma-se partir da hipótese de que depois de um tempo N ( normalmente maior que o prazo de depreciação contábil ), teremos, ainda, um Valor residual estimado (VRE). 

Depreciação LINEAR: Como no caso da Depreciação Contábil, a depreciação real anual é constante:

DL = (1/N ) . ( P – VRE)  

Aqui,  DL = Depreciação real Linear;

N = prazo de depreciação;

1/N = fator de depreciação;

P = Preço de compra;

VRE = Valor Residual Estimado.  

O Valor Real, depois de n anos é dado, então, por  

VL(n) = P – n . DL è VL(n) = P – . n  

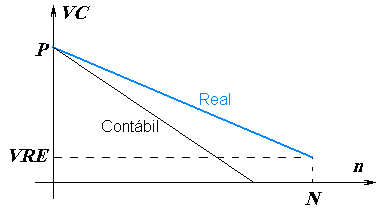
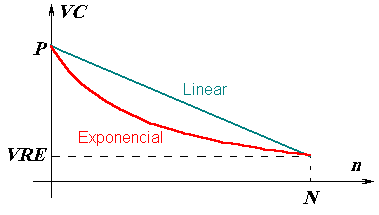
Graficamente, temos uma reta decrescendo de VL(0) = P até VL(N) = VRE. 

Podemos, novamente, considerar que com o passar dos anos, VL(n) forma uma Progressão Aritmética (PA), começando em VL(0) = P  e razão (VRE - P )/N.  

Percebe-se que no caso de VRE = 0, a Depreciação real Linear se comporta como a Contábil. 

Depreciação EXPONENCIAL: Neste caso, a depreciação real anual não é constante. 
Começa maior no primeiro ano e vai decrescendo exponencialmente:  

V(n) = P. E ⁿ è V(n) = P. ( 1 – t ) ⁿ  

Aqui,  V(n) = Valor real Exponencial após n anos;

P = Preço de compra;

E = ( 1 – t ) = base da Exponencial;

t = taxa de depreciação ( sobre o valor anterior ).  
 

A Depreciação real Exponencial é dada por D(n) = t . V(n-1)  

Graficamente, temos uma exponencial decrescendo de V(0) = P

até V(N) = VRE  è P. ( 1 – t ) ^N = VRE è  t = 1 -  

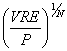
Podemos, agora, considerar que com o passar dos anos, V(n) forma uma Progressão Geométrica (PG), começando em V(0) = P  e razão ( 1 - t ):  

P ,  P. ( 1 – t )  ,  P. ( 1 – t ) ²  ,  P. ( 1 – t ) ² ,…, VRE

KOPITTKE, H. Bruno e CASAROTTO FILHO, Nelson. Análise de Investimentos. São Paulo: Atlas, 2000.

Voltar