FLUXO DE CAIXA

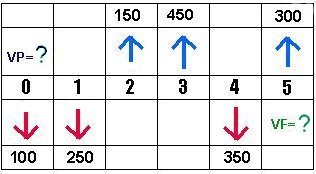
    O fluxo de caixa serve para demonstrar graficamente as transações financeiras em um período de tempo. O tempo é representado na horizontal dividido pelo número de períodos relevantes para análise. As entradas ou recebimentos são representados por setas verticais apontadas para cima e as saídas ou pagamentos são representados por setas verticais apontadas para baixo. Observe o gráfico abaixo:

    Estes valores não podem ser simplesmente somados ou subtraídos (a não ser com juros nulos), pois estão em tempos distintos e R$ 450 no 3º período não significam os mesmos R$450 em outros períodos; ele significa menos nos períodos anteriores e mais nos períodos seguintes,

    Por exemplo, com uma taxa de juros de 2% ao período, receber os R$450 no 3º período é equivalente a receber R$450x1,02 = R$459 no 4º período, ou R$459x1,02 = R$468 no 5º período ou  R$450/1,02 = R$441 no 2º período.

VALOR PRESENTE e VALOR FUTURO

    Chamamos de VP o Valor Presente, que significa o valor necessário na data 0 para que, considerando os juros ocorridos, represente o mesmo Capital que todas as entradas e saídas do Fluxo completo,

    Analogamente, VF é o Valor Futuro, que será igual ao valor que terei no final do fluxo, após juros, entradas e saídas. 

    Na fórmula M = P . (1 + i)ⁿ , o principal P é também conhecido como Valor Presente (PV = presentvalue) e o montante M é também conhecido como Valor Futuro (FV =future value). 

    Então essa fórmula pode ser escrita como  FV = PV (1 + i) ⁿ,ou simplesmente: 

    F = P (1 + i) ⁿ

    Isolando PV na fórmula temos PV = FV / (1+i)ⁿ,ou simplesmente: 

    P = F / (1+i)ⁿ

    Na HP-12C, o valor presente é representado pela tecla PV.

    Com esta mesma fórmula podemos calcular o valor futuro a partir do valor presente, para cada entrada ou saída do fluxo.

    Exemplo:

    Quanto representará, daqui a 12 meses, uma aplicação de R$1.500,00 a 2% ao mês?
    Solução:

         FV = 1500.(1 + 0,02)¹² = R$ 1.902,36

    Num fluxo, com várias entradas e saída, calculamos cada parcela no Presente ou no Futuro e somamos.

    Neste exemplo, com 2% ao período:

    VF = -100x1,02⁵- 250x1,02⁴ +150x1,02³ + 450x1,02² -350x1,02 + 300 = VP x1,02⁵ 

    VP = -100- 250/1,02 +150/1,02² + 450/1,02³ -350/1,02⁴ + 300/1,02⁵ = VF/ 1,02⁵ 

Fluxos Especiais

    Dois tipos de fluxo de caixa aparecem muitas vezes no comércio financeiro:

Fluxo UNIFORME 

   Um valor A sai (ou entra) todos os períodos de 1 a n. A Relação entre VP e A é:

   P = A/(1+i) +A/(1+i)² +A/(1+i)³+ A/(1+i)⁴ +... + A/(1+i)ⁿ 

    P = A. [ (1+i)^(n-1) + (1+i)^(n-2) +...  (1+i)² + (1+i)+ 1] / (1+i)ⁿ

   Entre os colchetes está a  Soma (na ordem inversa) de uma P.G com Primeiro termo = 1 e Razão =  (1+i)  

   P/A= [ (1+i)ⁿ  - 1] / [ i.(1+i)ⁿ ]

   Fluxo GRADIENTE  

   Um valor G no período 2; 2G,no período 3; 3G,no quarto e assim sucessivamente, até o período n

  A Relação entre VP e G é: 

    P = G/(1+i)² +2G/(1+i)³+3G/(1+i)⁴+... + (n-1)G/(1+i)ⁿ 

    P = G. [ (1+i)^(n-2) + 2(1+i)^(n-3) + 3(1+i)^(n-4)+ ... + (n-1)] / (1+i)ⁿ

  É possível provar que esta soma resulta em:

   P/G= [ (1+i)ⁿ  - 1 - n.i ] / [ i².(1+i)ⁿ]

Estas relações (P/A e  P/G), bem como outras (F/A, F/G, A/G, G/A,..) são tabeladas e servem para resolver inúmeros problemas de fluxo de caixa. 

Taxa Interna de Retorno (TIR)

   A  Taxa Interna de Retorno (TIR) de um Fluxo de Caixa é a taxa que ANULA o Valor Presente (e Futuro) deste Fluxo.

Voltar