Álgebra Linear
1. Preliminares
1.1.Anel: áC , + , . ñ é um
conjunto
C não vazio,
munido de duas operações ( + , . )
binárias (soma e produto) entre seus elementos, satisfazendo os seguintes axiomas:
C1:
Fechamento da soma
Þ a + b Î C , " a, b em
C
C2:
Fechamento do produto Þ a . b Î C , " a, b em
C
S1:
Associatividade da soma
Þ (a + b) + c = a + (b + c) , " a, b, c em C
S2:
Elemento neutro da soma
Þ $
z em C tq. z
+ a = a + z
= a , " a em
C
S3:
Comutatividade da soma
Þ a + b = b + a , " a, b em
C
S4:
Elemento inverso da soma
Þ $
sa em C tq. sa
+ a = a + sa
= z , " a em
C
D1:
Distributividade da soma
Þ a .(b + c) = a .b
+ a .c , " a, b, c em C
P1:
Associatividade do produto
Þ (a . b) . c = a .
(b . c) , " a, b, c em C
1.2.Exemplos:
Z
= Conjunto dos números inteiros,
Q = Conjunto dos números
racionais,
R = Conjunto dos números
reais,
C = Conjunto dos números
complexos,
M = Conjunto das matrizes com
valores em Z , Q , R ou C ,
P = Conjunto dos
polinômios com valores em Z , Q , R ou C ,
F = Conjunto das
funções com valores em Z , Q , R ou C ,
S = Conjunto das
seqüências com valores em Z , Q , R ou C ,
1.3. Anel
com Identidade:
P2:
Elemento neutro do produto
Þ $
u em C tq. u
. a = a . u = a , " a em C
1.4. Anel Comutativo:
P3:
: Comutatividade
do
produto Þ a . b = b . a , " a, b em
C
Obs.: M
deixa de ser
um exemplo.
1.5. Corpo:
é um Anel comutativo com identidade e
com
P4:
: Elemento inverso
do
produto Þ $
ia em C tq. ia
.
a = a .
ia
= u , " a em
C
Obs.: Z e P
deixam de
ser exemplos
2. Espaço Vetorial:
2.1. Definição:
áV, + , . ,
C ñ é um conjunto V não
vazio, munido de duas operações binárias ( + ,
. ) (soma e produto por escalar
do corpo C),
satisfazendo os seguintes axiomas:
V1:
Fechamento da soma
Þ v + w Î V , " v, w em
V
V2:
Fechamento do Produto Þ m . v Î V , " m em
C,
" v em
V
|
S1: Associatividade da soma
S2: Elemento neutro da soma
S3: Comutatividade da soma
S4: Elemento inverso da soma
|
M1: (m.n).v = m.(n.v)
M2: u.v = v
D1: m.(v+w) = m.v + m.w
D2: (m+n).v = m.v + n.v
|
2.2.
Exemplos: Q sobre
o corpo Q
R
, C
, Rn , Cn , P
, M
, F
ou S
sobre os corpos Q
, R
ou C
E
= Soluções de equações diferenciais homogêneas com dados nulos.
2.3. Espaço Vetorial Normado: é um espaço
vetorial V munido de uma
|
norma = || || : V
® [0 , ¥) tal que:
|
||
v || = 0 Û v = 0
||
m.v || = |m|. || v
||
|| v
+ w || £ || v || +|| w ||
|
|
Exemplos:
|
|| x ||
|
= | x |
em Q ou R
|
|
|
|| (a,b) ||
|
=
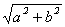 em
R2 »
C
em
R2 »
C
= | a | + | b |
= máx { | a | , | b | }
|
|
|
Idem
|
em
Rm , M , S
ou P
|
|
|
|| f || 2
|| f || p
|| f || ¥
|
= (ò |f(x)|².dx)1/2 em
P
ou F
= (ò |f(x)|p.dx)1/p
= max { |f(x)| }
|
|
|
|| c || p
|
= (S |ci|p)1/p em
S
|
2.4. Espaço Vetorial com
|
Produto Interno =
á
, ñ
: V x V ® C tal que:
|
á v, w
ñ =
á v, v
ñ ³
á v,
v
ñ =
|
á w, v ñ
0
0
Û
v
|
=
0
|
|
|
|
á m.v + w , x ñ
= m.
á v,
x
ñ + á w, x
ñ
|
|
Observ.: Num espaço vetorial
normado Þ
|
| á
v,
w
ñ
| £ || v || . || w ||
|
|
Um
produto interno induz uma norma Þ
|
|| v || = ( á
v,
v
ñ
)1/2
|
|
Exemplos:
|
á v, w ñ = v. w
em Q ou R
á v,
w
ñ = v.
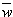 em C
em C
|
|
|
|
á (a,b), (c,d) ñ = a.c + b.d em
R2 »
C
|
|
|
|
Idem
em Rm, S
ou P
|
|
|
|
á f,
g
ñ = ò f(x).
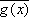 dx em
P ou F
dx em
P ou F
|
|
Perpendicularismo: Dizemos que u e v são perpendiculares se á v, w ñ = 0
2.5. Conjunto Linearmente Independente: Um
conjunto {v1,
v2, ... } de um
espaço vetorial é dito linearmente independente, se nenhum deles puder ser
expresso como combinação linear dos demais.
Equivalentemente: m1.v1 + m2.v2
+ ... = 0 Þ
m1 = m2
...
= 0
Exemplos:
Conjuntos Ortogonais = á
vm ,
vn ñ
= 0 sempre que m
¹
n
{
i, j, k }, { xk }, { ekx },
{ eikx }, { sen (kx) , cos (kx) },
Polinômios
de Legengre { Pk(x) } e
de Chebyshev { Tk(x) }
(Maple - Zip)
2.6. Base – dimensão: Um conjunto
linearmente independente, cujas combinações lineares geram todo o espaço
vetorial, é denominada Base do espaço vetorial.
Todas as possíveis bases de um mesmo espaço
vetorial devem ter a mesma quantidade
de elementos = Dimensão do espaço vetorial.
3. Transformações Lineares
3.1. Definição: Uma transformação T:
V1 ®
V2 é dita linear se
T(m.v + w) = m.T(v) + T(w), " m, v, w.
3.2.Exemplos:
Projeção
do Espaço num plano
Derivadas,
integrais
Séries
de Fourier
Multiplicação
por matrizes
Obs.:
Toda transformação linear pode ser representada pelo último exemplo.
|
0
0
0
0
|
1
0
0
0
|
0
2
0
0
|
0
0
3
0
|
.
|
a
b
c
d
|
=
|
b
2c
3d
0
|
pode
representar a derivada D dos
polinômios de grau 3 ou menor:
D( a + bx + cx² + dx³) = b + 2cx + 3dx²
|
Quando V1
= V2 ,dizemos que T
é um Operador linear.
Exemplos: Contração dilatação, rotação,
simetrias e cisalhamento no plano
3.3. Auto valores – auto vetores
Se, para algum escalar m
e para algum vetor v, tivermos
que T( v )
= m.v
dizemos
que v é um
auto vetor de T com relação ao auto valor m.
Exemplos:
os vetores do tipo v
= [ 2a
, 3a]
são auto vetores do cisalhamento dado por
T [
x,y
] = [x, x + y/3]
com relação ao auto valor 1.
os vetores do tipo v
= [ 0
, b] são auto vetores do mesmo
cisalhamento com relação ao auto valor 1/3.
as funções
C.ekt são auto funções
da derivada com relação ao auto valor k.
C.cos(mx)
são auto funções da 2ª
derivada com relação ao auto valor –m
².
4. Aplicação às EDPs Lineares
Seja, por exemplo, resolver a equação
Ft = 4Fxx Û
D1(F) = 4.D2(F)
Auto funções de
D1 :
F1
=
g(x) ekt
Û
D1( g(x)
ekt ) = k.g(x) ekt = k.F1
Auto
funções de
D2 : F2 =
f(t)
cos(mx) Û
D2( f(t)
cos(mx) )
= -m².f(t) cos(mx) = -m².F2
Igualando:
k.F1 =
4( -m².F2) Û
k.g(x)
ekt = -4m².f(t) cos(mx),
obtemos
que g(x) = cos(mx),
que
f(t)
= ekt e que k = -4m²
Portanto: F(t,x) = e-4m²tcos(mx) ou seus múltiplos (vale também para senos)
![]() em
R2 »
C
em
R2 »
C