Equação do Calor com barra

uma extremidade no gelo e outra isolada

por

Milton Procópio de Borba

> restart;

> Ate:=40:

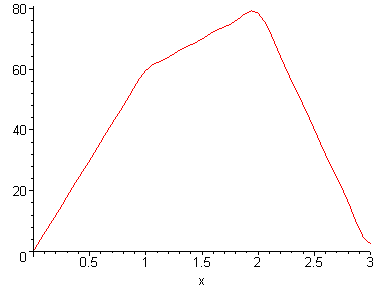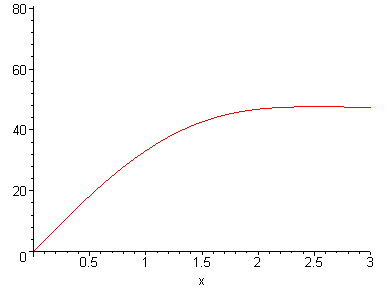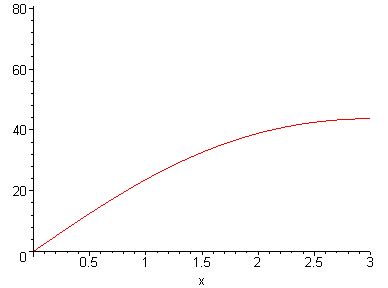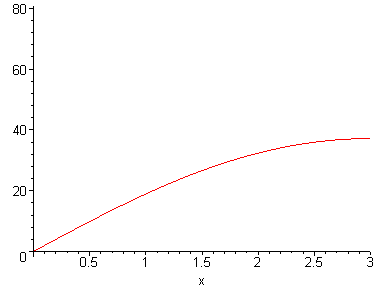
> T:=piecewise(x>=0 and x<=1,60*x, x>=1 and x<=2,20*x+40, x>=2 and x<=3,-80*x+240);

T := PIECEWISE([60*x, -x <= 0 and x-1 <= 0],[20*x+4...

> plot(T,x=0..3,color=blue);

[Maple Plot]

> s[n]:=sin(n*Pi*x/6);

> bn:=2*int(T*s[n],x=0..3)/3;

s[n] := sin(1/6*n*Pi*x)

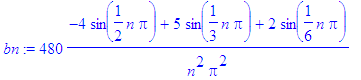
bn := 480*(-4*sin(1/2*n*Pi)+5*sin(1/3*n*Pi)+2*sin(1...

> for i from 1 to Ate by 2 do

> B:=subs(n=i,bn):

> b[i]:=evalf(B)

> od;

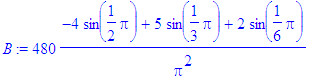
B := 480*(-4*sin(1/2*Pi)+5*sin(1/3*Pi)+2*sin(1/6*Pi...

b[1] := 64.68962112

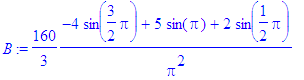
B := 160/3*(-4*sin(3/2*Pi)+5*sin(Pi)+2*sin(1/2*Pi))...

b[3] := 32.42277875

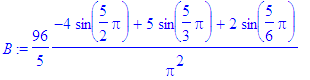
B := 96/5*(-4*sin(5/2*Pi)+5*sin(5/3*Pi)+2*sin(5/6*P...

b[5] := -14.25978520

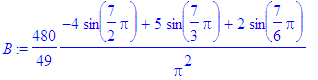
B := 480/49*(-4*sin(7/2*Pi)+5*sin(7/3*Pi)+2*sin(7/6...

b[7] := 7.275400611

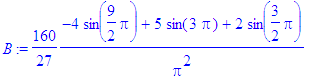
B := 160/27*(-4*sin(9/2*Pi)+5*sin(3*Pi)+2*sin(3/2*P...

b[9] := -3.602530973

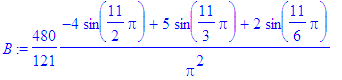
B := 480/121*(-4*sin(11/2*Pi)+5*sin(11/3*Pi)+2*sin(...

b[11] := -.5346249680

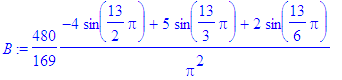
B := 480/169*(-4*sin(13/2*Pi)+5*sin(13/3*Pi)+2*sin(...

b[13] := .3827788231

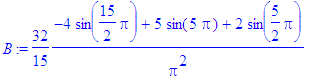
B := 32/15*(-4*sin(15/2*Pi)+5*sin(5*Pi)+2*sin(5/2*P...

b[15] := 1.296911150

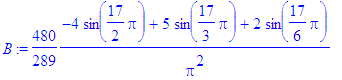
B := 480/289*(-4*sin(17/2*Pi)+5*sin(17/3*Pi)+2*sin(...

b[17] := -1.233545432

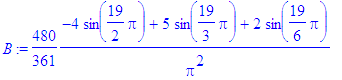
B := 480/361*(-4*sin(19/2*Pi)+5*sin(19/3*Pi)+2*sin(...

b[19] := .9875197504

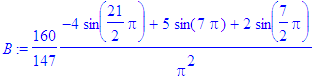
B := 160/147*(-4*sin(21/2*Pi)+5*sin(7*Pi)+2*sin(7/2...

b[21] := -.6616893623

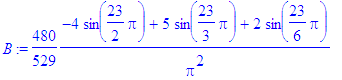
B := 480/529*(-4*sin(23/2*Pi)+5*sin(23/3*Pi)+2*sin(...

b[23] := -.1222866184

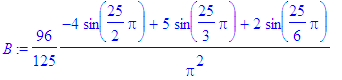
B := 96/125*(-4*sin(25/2*Pi)+5*sin(25/3*Pi)+2*sin(2...

b[25] := .1035033938

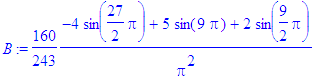
B := 160/243*(-4*sin(27/2*Pi)+5*sin(9*Pi)+2*sin(9/2...

b[27] := .4002812192

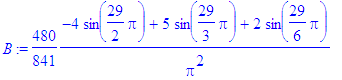
B := 480/841*(-4*sin(29/2*Pi)+5*sin(29/3*Pi)+2*sin(...

b[29] := -.4238937336

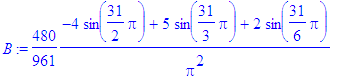
B := 480/961*(-4*sin(31/2*Pi)+5*sin(31/3*Pi)+2*sin(...

b[31] := .3709621539

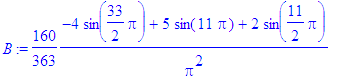
B := 160/363*(-4*sin(33/2*Pi)+5*sin(11*Pi)+2*sin(11...

b[33] := -.2679568492

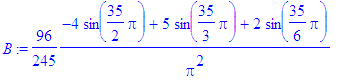
B := 96/245*(-4*sin(35/2*Pi)+5*sin(35/3*Pi)+2*sin(3...

b[35] := -.5280785398e-1

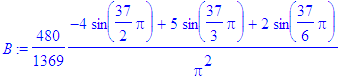
B := 480/1369*(-4*sin(37/2*Pi)+5*sin(37/3*Pi)+2*sin...

b[37] := .4725319293e-1

B := 160/507*(-4*sin(39/2*Pi)+5*sin(13*Pi)+2*sin(13...

b[39] := .1918507618

> ser_Cal:=0:

> for n from 1 to Ate by 2 do

> ser_Cal:=ser_Cal + exp(-t*(n*Pi/6)^2)*b[n]*sin(n*Pi*x/6):

> od:

> with(plots):

> G1 := plot(T,x=0..3,color=blue,style=point):

> ser:=subs( t=0, ser_Cal):

> G2:=plot(ser,x=0..3):

> display({G1,G2}); 

Warning, the name changecoords has been redefined

[Maple Plot]

 

Gráfico da Equação do Calor na Barra

> plot3d(ser_Cal,x=0..3,t=0..5,axes=boxed);

[Maple Plot]

 

> animate(ser_Cal,x=0..3,t=0..2,frames=100);

Voltar