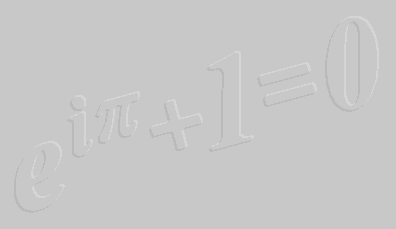
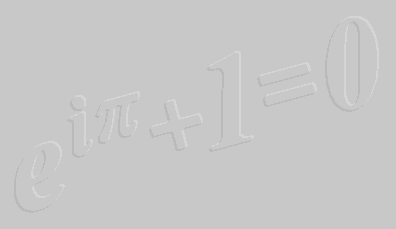
Esta equação foi escolhida por ser verdadeira*
e envolver os sete (7) principais símbolos da Matemática:
e ® base dos logaritmos naturais (número de Euler)
i ® base dos números imaginários ( i² = -1 )
p ® razão entre a circunferência e o seu diâmetro ( C = p d )
1 ® elemento neutro da multiplicação ( k x 1 = k )
0 ® elemento neutro da soma ( k + 0 = k )
+ ® sinal da soma ( base das demais operações )
= ® sinal de igualdade
(*) Demostração:
Por Maclaurin: ex = 1 + x + x²/2 + x³/6 + ... + xn /n! + ...
Com x = iq, temos: eiq = 1 + iq + (iq)²/2 + (iq)³/6 + ... + (iq)n /n! + ...
Usando i² = -1, i³ = -i, i4 = 1, i5 = i, i6 = -1, ..., conseguimos:
eiq = 1 + iq - q²/2 - iq³/6 + q 4/24+iq 5/5! - q 6/6! - iq 7/7! +... +/- ...
eiq = 1- q²/2 + q 4/24- q 6/6! + q 8/8! - ... +/- ... + i(q - q³/6 + q 5/5!- q 7/7! + q 9/9! - ... +/- ...)
e chegamos na
Relação de Moivre: eiq = cos q + i sen q ,pois, também por Maclaurin:
cos q = 1- q²/2 + q 4/24- q 6/6! + q 8/8! - ... +/- ...
sen q = q - q³/6 + q 5/5!- q 7/7! + q 9/9! - ... +/- ...
Fazendo q = p, na relação de Moivre: eip = cos p + i sen p
Ou seja, eip = -1+ i 0 Þ eip = -1 Þ eip +1=0