Para motivar a discussão, iremos formular um problema simples de programação linear envolvendo duas variáveis de decisão e três restrições, obtendo a solução gráfica de forma semelhante àquela utilizada no exemplo da Duas Minas (Word_ZIP ou Maple_ZIP ou Excel_ZIP)

Suponha que temos uma empresa que produz carros de brinquedo e trens de brinquedo. O Departamento de Contabilidade analisou os custos e lucros e determinou que para cada carro produzido (e imediatamente vendido) havia um lucro de $30, e para cada trem, $40. Temos dois departamentos onde esses brinquedos são produzidos. O departamento de carros tem uma capacidade de produção diaria de 90 unidades, e o departamento de trens, 60 unidades. Um fator complicante na produção destes brinquedos é uma parte especial que deve ser comprada de um fornecedor externo que pode fornecer somente 600 unidades por dia. Segundo o departamento de engenharia, cada carro necessita 5 partes, e cada trem 6 partes. Temos que determinar a produção diária de carros e trens de forma a maximizar o lucro diário.

Neste problema temos duas variáveis de decisão:

- número de carros / dia

- número de trens / dia

A função-objetivo a ser maximizada é o lucro diário, dado por:

.

Nossas restrições são dadas por

, - limites de capacidade de produção de cada departamento,

- limites das peças especiais.

Temos ainda as restrições naturais , .

Ver solução no Excel 

Solução Gráfica

Como temos somente duas variáveis de decisão, a solução gráfica é viável, de modo que podemos proceder como no caso da Companhia de Duas Minas.

Vamos obter inicialmente a região factível:

> restart:

> with(plots):

Warning, the name changecoords has been redefined

> Rest:=[5*x1+6*x2<=600,x1<=90,x2<=60,x1>=0,x2>=0];

> Regiao_factivel:=inequal(Rest, x1=0..130,x2=0..80, optionsfeasible=(color=blue),optionsexcluded=(color=white)):

>

>

> display([Regiao_factivel]);

>

Vamos agora inserir neste gráfico algumas retas correspondendo a valores particulares de lucro diário:

> curvas_de_lucro:=contourplot(30*x1+40*x2,x1=0..140,x2=0..120,contours=[1800,3000,4000],linestyle=4,numpoints=1000,color=black):

> display([Regiao_factivel,curvas_de_lucro]);

Observe que a linha correspondente a z = 4000 corresponde a uma solução não factível para o problema. É óbvio neste problema que a solução factível que maximiza o lucro é aquela que passa pelo vértice dado pela intersecção da reta com a reta :

> sol:=solve({5*x1+6*x2 = 600,x2=60},{x1,x2});

> assign(sol);

Com essa solução o lucro será

> z:=30*x1+40*x2;

>

De fato, podemos verificar o resultado no gráfico.

> unassign('x1', 'x2'):

> lucro_maximo:=implicitplot(30*x1+40*x2=3840,x1=0..140,x2=0..120,linestyle=3,numpoints=1000,color=red):

> display([Regiao_factivel,lucro_maximo]);

Um modo mais compacto para fazer o cálculo anterior é

> with(simplex):

Warning, the name display has been redefined

Warning, the protected names maximize and minimize have been redefined and unprotected

> solve(convert({Rest[1],Rest[3]},equality));

> assign(%):

> z:=30*x1+40*x2;

> x1:='x1':x2:='x2':

A região factível no exemplo acima é um exemplo de região convexa. Vamos definir formalmente o conceito de região convexa e ponto extremo de uma região convexa.

Definição 1 Um conjunto F é dito convexo se para quaisquer dois pontos x1 e x2 em F, o segmento que liga os dois pontos está inteiramente dentro de conjunto, ou seja, x = 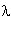(x1 - x2) + x2 pertence a F para £ 1.

Intuitivamente um conjunto convexo não pode ter buracos, e suas fronteiras devem ser planas e retas ligando dois vértices quaisquer não devem sair do polígono.

Definição 2 Um ponto x é dito ser um ponto extremo de um conjunto convexo se e somente se não há outros pontos x1 e x2 (x1 <> x2) no conjunto tais que x = x1 + (1- ) x2 , £ 1.

Intuitivamente, um ponto extremo não pode estar situado "entre" dois outros pontos do conjunto.

É possível mostrar que, em problemas de programação linear, as regiões factíveis são sempre convexas. Além disso, se a região convexa factível correspondente ao problema de programação linear é não vazia, ela deve ter ao menos um extremo. Além disso, se há uma solução finita ótima para o programa linear, então esta solução deve ser um ponto extremo da região factível. No nosso exemplo anterior a região factível possui 5 pontos extremos. Formalmente deveríamos testar todos os pontos extremos, mas normalmente, em problemas 2-dimensionais o método gráfico-visual é apropriado, especialmente quando o número de restrições (número de pontos extremos) é muito alto.

Por outro lado, se temos n = 3 variáveis de decisão torna-se mais difícil a visualização. Para n >3 ela é impossível. Modelos de problemas da vida real podem ter até milhares de variáveis e condições de restrição. Neste caso é utilizada uma técnica matemática denominada método simplex .

Warning, the name changecoords has been redefined