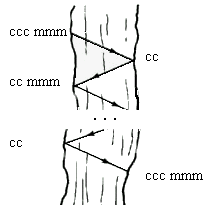
Problema dos canibais e dos missionários

Três canibais e três missionários estão viajando juntos e chegam à margem de um rio. Eles desejam atravessar para a outra margem para, desta forma, continuar a viagem. O único meio de transporte disponível é um barco que comporta no máximo duas pessoas. Há uma outra dificuldade: em nenhum momento o número de canibais pode ser superior ao número de missionários pois desta forma os missionários estariam em grande perigo de vida. Como administrar a travessia?

Para resolver este problema, considere inicialmente as situações (ou estados) que podem ocorrer numa das margens no que se refere ao número de canibais e missionários. Podemos representar cada um destes estados por um par ordenado (c,m), onde c e m representam o número de canibais e de missionários, respectivamente. Desde que 0 =< c <= 3 e que 0 =< m <= 3, há, no total, 16 possíveis estados, que vão de (0,0) a (3,3).

Contudo, alguns destes estados não são viáveis em função da restrição imposta pelo problema de que em nenhum momento o número de canibais pode ser superior ao número de missionários. É o caso dos pares ordenados (2,1), (3,1) e (3,2), assim como dos pares (1,2), (0,2) e (0,1). Nestes últimos três casos, a restrição se verifica na margem oposta, já que os canibais e missionários restantes (complemento em relação a (3,3)) estão lá.

Conhecidos os estados viáveis, podemos, agora, estabelecer as condições que definem as possíveis transições entre estes estados, ou seja, as travessias do barco de uma margem para a outra.

Um modelo para este problema é definir o grafo G(V,A) como:

V = { (c,m) | c e m representam o número de canibais e de missionários numa das margens do rio, sendo que: 

A = { (e1,e2) | e1 = (c1,m1) é o estado da margem onde o barco está antes da travessia ser iniciada, e e2 = (c2,m2) é o estado da margem oposta após o barco completar a travessia, sendo que: 

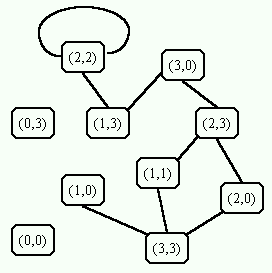As primeiras duas condições acima afirmam que após a travessia os números de canibais e de missionários da margem oposta não podem ser menor do que os números que haviam antes da travessia. Por sua vez, a terceira condição restringe o número de pessoas que pode ir no barco. Note que a relação acima é simétrica, motivo pelo qual aparece o operador de módulo na terceira restrição.

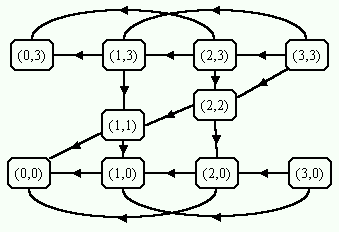
O grafo ao lado apresenta todas as possíveis transições entre estados. Buscar uma solução neste grafo implica em  procurar uma cadeia de tamanho impar que parta do vértice (3,3) (todos os canibais e os missionários estão numa margem) e que chegue novamente ao vértice (3,3) (todos os canibais e os missionários estão na outra margem). 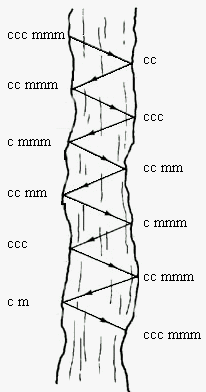A cadeia precisa ser impar pois o barco deve fazer um conjunto de idas e voltas, sendo necessária uma última travessia para levar os remanescentes para a outra margem. Uma das soluções possíveis é apresenta a seguir (figura da esquerda), juntamente com sua interpretação (figura da direita).

Um segundo modelo para este problema é dado pelo grafo G(V,A):

V = { (c,m) | c e m representam o número de canibais e de missionários na margem esquerda do rio, sendo que: 

A = { (e1,e2) | e1 = (c1,m1) é o estado antes da travessia ser iniciada, estando o barco na margem esquerda, e e2 = (c2,m2) é o estado após o barco completar a travessia, sendo que: 

Diferentemente do modelo anterior, os vértices agora sempre representam o estado da margem esquerda. Se necessário, o estado da margem direita pode ser obtido obtendo-se o complemento em relação a (3,3). Apesar das restrições quanto aos vértices válidos serem as mesmas, as condições para as transições foram adaptadas à nova definição dos vértices. Em particular há que se notar que a relação entre os estados deixou de ser simétrica.

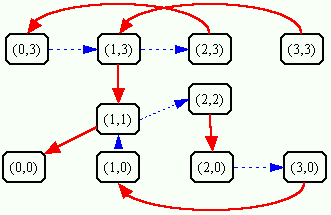
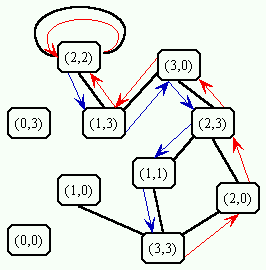
Para se obter uma solução segundo este modelo é necessário procurar um caminho que parta do vértice (3,3) (todos os canibais e os missionários estão na margem esquerda) e que chegue ao vértice (0,0) (não há mais nenhum canibal ou missionário na margem esquerda). Como no grafo só estão representadas as idas do barco da margem esquerda para a direita, neste caminho devem alternadamente percorrer uma aresta segundo sua orientação (a ida, em vermelho) para em seguida percorrer uma outra aresta no sentido contrário de sua orientação (a volta, em azul). A mesma soluções obtida pelo modelo anterior é apresentada a seguir.

Voltar