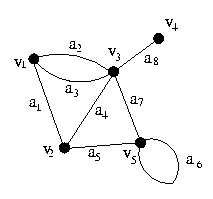
Um grafo G = (V,E) é um conjunto não-vazio V, cujos elementos são chamados vértices, e um conjunto E de arestas. Uma aresta é um par não-ordenado (vi,vj), onde vi e vj são elementos de V. Normalmente, utiliza-se uma representação gráfica de um grafo. Eis um exemplo de grafo, com a sua representação gráfica:
V = {v1, v2, v3, v4,
v5}
E = {a1, a2, a3,
a4, a5, a6, a7, a8}
onde a1 = (v1,v2), a2 =
(v1,v3), a3 = (v1,v3),
a4 = (v2,v3), a5 =
(v2,v5), a6 = (v5,v5),
a7 = (v3,v5), a8 =
(v3,v4).

Figura 1
Note que nessa definição são permitidos laços (veja a aresta a6) e arestas paralelas (as arestas a2 e a3, por exemplo). Um grafo que não contém nenhum laço e nenhumas arestas paralelas é chamado grafo simples. Essa definição não impede que um grafo seja infinito. Mas esse tipo de grafo não será estudado aqui. Um grafo que contém no mínimo um laço é um pseudografo. Um grafo que contém arestas paralelas é um multigrafo.
O problema das pontes de Königsberg é um problema antigo que foi resolvido por Euler, com a criação da teoria dos grafos. O problema é o seguinte. Considerando um rio com duas ilhas e 7 pontes como ilustrado na figura 2, é possível identificar um caminho que atravesse todas as pontes uma vez só e que retorne ao ponto de partida?

Figura 2
Para resolver esse problema, Euler o representou com o grafo ilustrado na figura 3. Com essa representação, e considerando as propriedades do grafos que serão apresentadas mais tarde nesse curso, é possível resolver facilmente esse problema.
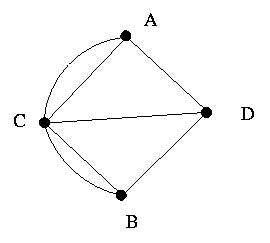
Figura 3
Mais detalhes sobre As pontes de KönigsbergUm grafo completo com v vértices, escrito Kv, é um grafo simples onde todo par de vértices é ligado por uma aresta. Em outras palavras, um grafo completo é um grafo simples que contém o número máximo de arestas.
Teorema 1-1: O número de arestas em um grafo completo é
n(n-1)/2.
Prova: A prova é por indução matemática. Chamaremos Gn um grafo que contém n vértices. Consideramos primeiro o caso trivial, o grafo G1. Nesse caso, como existe somente um vértice, é impossível definir uma aresta que não seja um laço. Então não pode existir nenhuma aresta, e verificamos que n(n-1)/2 = 0.
Suponhamos que a hipótese é verdadeira para Gn, onde n 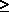 1. Seja agora o grafo Gn+1. Precisamos
provar que o número de vértices nesse grafo é n(n+1)/2. Seja vn+1 o
vértice adicional que se encontra em Gn+1 e não em Gn. O
número máximo de arestas no grafo Gn+1 é igual ao número máximo no
grafo Gn mais todas as ligações possíveis entre vn+1 e
cada vértices de Gn. Como esse número de ligações é igual ao número
de vértices em Gn, temos:
1. Seja agora o grafo Gn+1. Precisamos
provar que o número de vértices nesse grafo é n(n+1)/2. Seja vn+1 o
vértice adicional que se encontra em Gn+1 e não em Gn. O
número máximo de arestas no grafo Gn+1 é igual ao número máximo no
grafo Gn mais todas as ligações possíveis entre vn+1 e
cada vértices de Gn. Como esse número de ligações é igual ao número
de vértices em Gn, temos:
| Número máximo = | n(n-1) | + n = | n(n-1) + 2n | = | n2+n | = | n(n+1) |
| 2 | 2 | 2 | 2 |
Uma outra maneira de chegar a esse resultado e considerar o fato que o número de arestas em um grafo completo de n vértices corresponde a todos os pares possíveis uv, onde u e v são vértices. Assim, o número de vértices é:
![]()
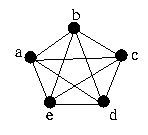
Eis alguns exemplos de grafos completos:
Figura 4
O grafo K1 é chamado grafo trivial.
Seja dois vértices vi e vj, e uma aresta ak = (vi,vj). A aresta ak é dita incidente a ambos vértices vi e vj. Duas arestas não paralelas que são incidentes a um mesmo vértice são ditas adjacentes. Dois vértices que são ligados por uma mesma arestas também são ditos adjacentes. O número de arestas incidentes a um vértice vi (contando duas vezes os laços) é chamado o grau do vértice vi: d(vi). Na figura 1, por exemplo, temos d(v1)=3, d(v5)=4 e d(v4)=1.
Suponhamos agora um grafo G com a arestas e v vértices v1, v2..., vn. Como cada aresta contribui para dois graus, a soma dos graus de todas as arestas de G é duas vezes o número de arestas:
|
n |
d(vi) = 2a |
Teorema 1-2: O número de vértices de grau ímpar de um grafo é
sempre par.
Prova: Separando os vértices de grau par e os de grau ímpar, a soma pode ser separada em duas somas:
|
n |
d(vi) = |
|
d(vk) + |
|
d(vl) |
Como a soma na esquerda é par (=2a) e a primeira soma do lado de direita também é par, por ser uma soma de números pares, a segunda também tem que ser par:
|
|
d(vl) = um número par |
Como todo valor vl é ímpar, a quantidade de itens na soma tem que
ser par. 
Um vértice que possui grau zero é um vértice isolado. É possível que um grafo não contenha nenhuma aresta. Nesse caso todos os vértices são isolados e o grafo é chamado grafo nulo. Um grafo no qual todos os vértices têm o mesmo grau r é chamado grafo regular de grau r. Por exemplo, o grafo K5 da figura 4 é um grafo regular de grau 4.
Eis algumas definição de operações sobre grafos que serão uteis mais para frente:
 E2 é vazio.
E2 é vazio.
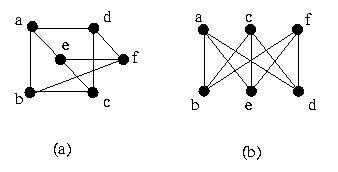
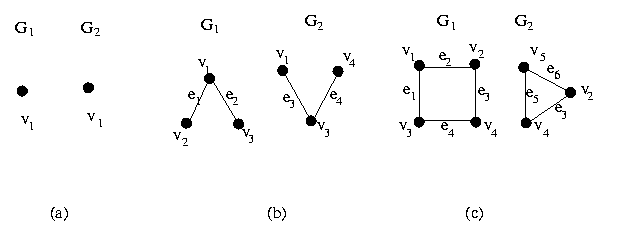
Dois grafos G1(V1,E1) e G2(V2,E2) são ditos isomorfos entre si se existe uma correspondência entre os seus vértices e arestas de tal maneira que a relação de incidência seja preservada. Em outros termos, temos |V1|= |V2| e existe uma função unívoca f: V1-->V2, tal que (i,j) é elemento de E1 se e somente se (ƒ(i),f(j)) é elemento de E2. Eis alguns exemplos de grafos isomorfos:
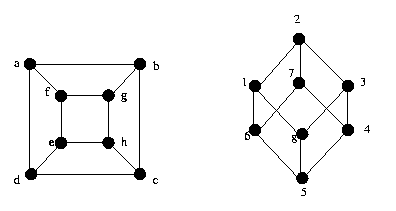
Figura 5
Para ver o isomorfismo dos grafos da figura 5, podemos utilizar a seguinte função:
f(a) = 1, f(b) = 2, f(c) = 3, f(d) = 8, f(e) = 5, f(f) = 6, f(g) = 7, f(h) = 4.
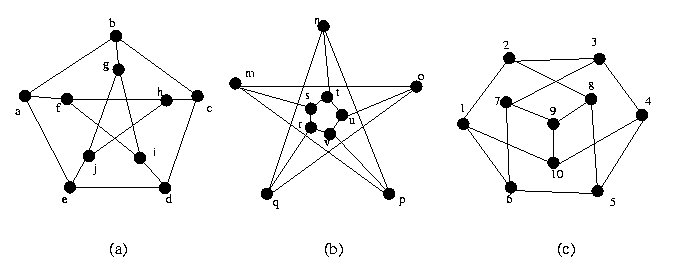
Figura 6
Para ver o isomorfismo dos grafos 6(a) e 6(b), utilize a seguinte função:
f(a) = s, f(b) = t, f(c) = u, f(d) = v, f(e) = r, f(f) = m, f(g) = n, f(h) = o, f(i) = p, f(j) = q
Para ver o isomorfismo dos grafos 6(a) e 6(c), utilize a seguinte função:
f(a) = 1, f(b) = 10, f(c) = 4, f(d) = 5, f(e) = 6, f(f) = 2, f(g) = 9, f(h) = 3, f(i) = 8, f(j) = 7.
Esses exemplos devem ser suficientes para mostrar que não é sempre fácil determinar se dois grafos são isomorfos. Não existe atualmente um algoritmo eficiente para resolver esse problema. Poderiamos tentar todas as permutações possível, mas isso daria um algoritmo de complexidade em O(n!). Para que dois grafos sejam isomorfos, no mínimo essas condições tem que ser respeitadas:
Note que isso não é suficiente par que sejam isomorfos. Por exemplo, os grafos da figura 7 respeitam essas condições e não são isomorfos.
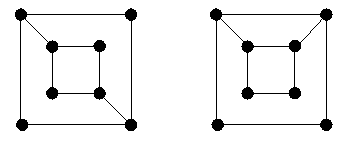
Figura 7
Mesmo se ambos grafos são regulares de grau k, as condições acima não são suficientes para concluir que eles são isomorfos. Veja o exemplo da figura 7'. É muito fácil ver que eles não são isomorfos apesar de que os dois são regulares de grau 3.
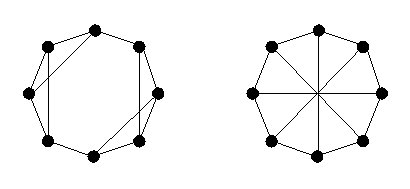
Figura 7'
Para determinar se um grafo é isomorfo, existe uma técnica (não fácil de
implementar!) que consiste em modificar a maneira de desenhar um grafo para
torná-lo igual ao outro, com a exceção dos rótulos dos vértices. Para explicar
melhor isso, vamos ver como o grafo da figura 6a pode ser tranformado em um
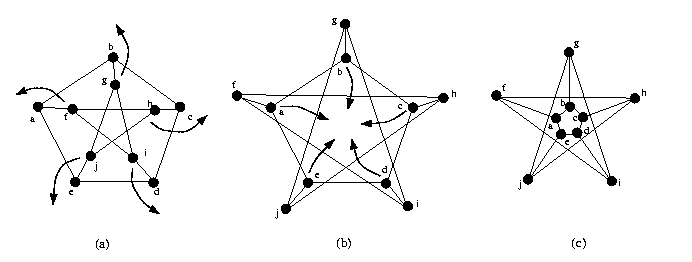
grafo equivalente ao grafo da figura 6b. Como ilustrado na figura 8, começamos
colocando fora os vértices f, g, h, i e j para obter o grafo 8b.
Depois, colocamos os vértices a, b, c, d e Figura 8 O vetor de grau d(G) de um grafo G é a sequência dos graus dos
vértices de G em ordem não crescente. Note que dois grafos não isomorfos podem
ter o mesmo vetor de grau. Por exemplo, o vetor de grau do grafos dos figura 7 é
o seguinte: [3,3,3,3,2,2,2,2].
Uma questão interessante é saber se um dado vetor é um vetor gráfico,
isto é, um vector tal que é possível desenhar um grafo usando os valores que ele
contém. Isso poderia ser útil, por exemplo, para testar se não houve erro na
produção de uma representação interna de uma grafo no computador.
Já podemos identificar algumas propriedades essenciais para que um vetor de
grau represente um grafo. A somatória dos valores dever ser par e o número de
valores ímpares deve ser par. Se o grafo representado deve ser simples, cada
valor não pode ultrapassar n-1, onde n é o número de valores
contidos na sequência. Mas isso não é suficiente. Considere por exemplo a
sequência [3,3,1,1]. É fácil conferir que ela respeita todas as condições
e entretanto não é um vetor gráfico. O Teorema 1-3 indique como determinar se um
vetor de grau é gráfico:
Teorema 1-3: Um vetor de grau S = [d1, d2,
..., dn] é gráfico se e somente se a sequência S 1 =
[d2-1, d3-1, ..., dd 1+1-1,
dd 1+2, ..., dn], após ordenação em ordem não
crescente, é gráfica. Prova:
Ida: Primeiro, devemos entender a idéia atrás desse teorema. Retirando
o primeiro valor do vetor, o que de fato é equivalente a retirar o vértice do
grafo que tem o maior grau, devemos subtrair 1 a d1 vértices
do grafo resultante. O Teorema diz que se fizermos isso para os
d1 vértices de maior grau (representados pelos
d1 próximos valores da sequência), o resultado é um vetor
gráfico.
Seja um grafo G que corresponde ao vetor S. Tem dois casos a considerar. Se o
vértice v que corresponde a d1 é efetivamente ligado
aos vértices que correspondem aos d1 próximos valores da
sequência, não tem nada a provar, pois é evidente que nesse caso o grafo
resultante depois de remoção de v corresponde ao vetor S1.
Suponhamos agora que v é ligado a um vertice u que não corresponde
a um dos valores modificados da sequência. Isso significa que existe um vértice
w não ligado a v que corresponde a um dos valores de maior grau.
Vamos mostrar que é possível modificar G de tal maneira que w seja ligado
com v e u não ligado com v, conservando o mesmo vetor de
grau. Fazendo assim com todos os vértices ligados a v que não são na
lista dos vértices de maior grau, voltaremos ao outro caso que já foi
considerado.
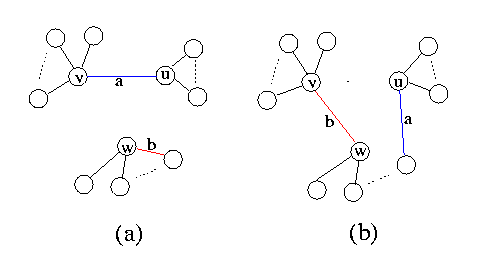
Considere a figura 8'a, onde a é a aresta que liga v e u
e b é a aresta que liga w com um de seus vértices adjacentes. Para
transformar o grafo, é só usar a outra extremidade de b para ligar
w com v. Ao mesmo tempo, deslocamos a extremidade da aresta
a de v para o vértice que foi desligado de w. Podemos
conferir facilmente que nada mudo na sequência de valores, todos os vértices
envolvidos nessa mudança conservam o mesmo grau.
Figura 8' Volta: Deixamos essa prova como exercício.
Um grafo G2(V2,E2) é um subgrafo de um grafo
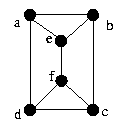
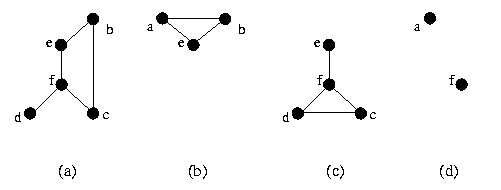
G1(V1,E1) se V2 Considere agora o grafo ilustrado na figura 9. Na figura 10 são ilustrados
quatro subgrafos desse grafo. Em 11a temos um subgrafo que não tem nada de
especial. O grafo ilustrado em 11b é uma clique, o subgrafo 10c e um grafo
induzido pelos vértices c,d,e e f, e o último é um conjunto
independentes de vértices.
Figura 9 Figura 10 Um caminho em um grafo G = (V,E) é uma seqüência de vértices
v1,...vn, tal que (vi,vi+1) é um
elemento de E, para 1 No grafo ilustrado na figura 9, a seqüência [a,e,f,c] é um caminho simples e
também um trajeto. A seqüência [a,e,b,a,d] é um trajeto mas não um caminho
simples.
Um caminho onde o primeiro vértice da seqüência é igual ao último é um
circuito, se todas as arestas são distintas. Se além disso, não há
vértice repetido no circuito, digamos que ele é um ciclo. Na figura 9, a
seqüência [a,b,c,f,e,a] é um ciclo: nenhum vértice se repete, com a exceção dos
primeiro e último. Um exemplo de circuito que não é um ciclo é a seqüência
[a,b,d,a,c,e,a] do grafo completo da figura 11.
Figura 11 Figura 12 Teorema 1-4: Se um grafo (conexo ou desconexo) contém exatamente
dois vértices de grau ímpar, existe um caminho ligando esses dois vértices.
Prova: Seja G um grafo onde todos os vértices são de grau par, exceto
os vértices v1 e v2. Segundo o teorema 1-2, não existe um
grafo (ou um componente) que tem um número ímpar de vértices que possuem grau
ímpar. Então v1 e v2 devem pertencer ao mesmo componente,
e deve existir um caminho entre eles.
Um grafo bipartite é um grafo G = (V,E) cujo conjunto de vértices V pode ser
separado em dois conjuntos X e Y, tal que toda aresta de E liga somente vértices
de X com vértices de Y.
A figura 13a ilustra um grafo bipartite. Isso fica evidente se consideramos o
grafo 13b que é isomorfo.
Figura 13 Existe um teorema interessante em relação ao grafo bipartite:
Teorema 1-5: Um grafo G é bipartite se e somente se todo ciclo de G
possuir comprimento par. Prova:
Ida: Seja X e Y as duas partições de G. Todo caminho em G alterna um
vértice de X com um vertice de Y. Isso é a conseqüência da definição de grafo
bipartite. Supondo que um ciclo contém um vértice vi em uma das duas
partições. Para voltar a esse vértice, é preciso ir na outra partição e voltar
um número par de vezes.
Volta: Seja G um grafo onde todo ciclo é de comprimento par. Seja um
vértice vi de G. Colocamos num conjunto X o vértice vi e
todos os outros que são a uma distância par de vi. Os outros vértices
formam o conjunto Y. Se não tivesse nenhuma aresta ligando dois vértices de X ou
dois vértices de Y, respeitariamos as condições para que o grafo seja bipartite.
Suponhamos agora que existe uma outra aresta entre dois vértices a e
b de X (ouY). Já temos um caminho par entre a e b.
Acrescentando a nova aresta, obteriamos um ciclo de comprimento ímpar, o que
contradiz a hipótese. Portanto, nõa pode existir outra aresta entre qualquer par
de vértice que já está em X (igualmente par Y) e o grafo é bipartite.
Note que essa prova indica de maneira direta qual seria o algoritmo par
determinar se um grafo é bipartite ou não.
A noção de grafo completo pode ser extendido aos grafos bipartites. Um
grafo bipartite completo é um grafo onde todos os vértices da partição X
é ligado por uma aresta a todos os vértices da partição Y. Seja m e
n o número de vértices em X e Y, respectivamente, o grafo completo
bipartite sera denotado Km,n. Por exemplo, o grafo da figura 13b é
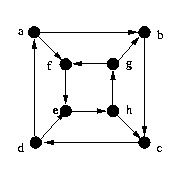
K3,3. Figura 14 V = {a,b,c,d,e,f,g} Teorema 1-6: A soma dos graus de saída (de entrada) de um grafo
direcionado é igual ao número de arestas no grafo.
É muito fácil se convencer do teorema 1-6, considerando que cada aresta
contribui exatamente para um grau de entrada e um grau de saída.
O grafo obtido substituindo cada aresta de um grafo direcionado G por uma
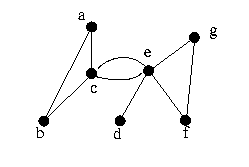
aresta não direcionada é chamado grafo subjacente de G. a figura 14'
ilustra o grafo subjacente do grafo da figura 14.
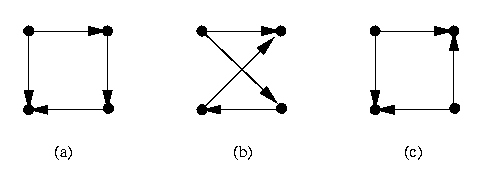
Figura 14' A noção de isomorfismo pode ser extendida aos grafos direcionados. Nesse
caso, devemos tomar cuidado para considerar também a orientação das arestas. Por
exemplo, o grafo (a) da figura 14'' é isomorfo ao grafo (b) mas não ao grafo
(c).
Figura 14'' Um grafo é conexo se o seu grafo subjacente é conexo. Intuitivamente
isso corresponde à característica do grafo constituir um pedaço só. Um grafo
direcionado onde existe um caminho entre qualquer par de vértices é dito
fortemente conexo.
Um problema interessante é saber se um grafo não direcionado pode ser
transformado em grafo fortemente conexo, trocando cada aresta por uma aresta
orientada. Sabendo que uma ponte é uma aresta que torna um grafo
desconexo se ela for retirada, temos um teorema interessante nesse respeito:
Teorema 1-7: É possível orientar as arestas de um grafo conexo não
direcionado de tal maneira a obter um grafo direcionado fortemente conexo se e
somente se o seu grafo subjacente não contém nenhuma ponte.
Prova:
Ida: Suponhamos um grafo fortemente conexo que contém no mínimo uma
ponte. Deve existir no grafo no mínimo dois vértices cuja ligação exige passar
por essa ponte. Necessariamente essa ponte permite caminhar em uma direção, por
exemplo de um vértice vi para outro vértice vk, mas não
permite o retorno de vk para vi.
Volta: Como o grafo não contém nenhuma ponte, toda aresta faz parte de
um ciclo. Suponhamos tal ciclo, que chamaremos C1, e orientemos as
arestas de tal maneira que seja possível percorrer o ciclo e voltar à origem. É
claro que em C1 todo vértice é acessível a partir de qualquer outro.
Consideremos agora um outro ciclo C2 do grafo que tem no mínimo um
vértice em comum com C1. Orientamos as arestas da mesma maneira, mas
sem mudar a orientação das arestas de C2 que já existem em
C1. É evidente que qualquer vértice do grafo obtido combinando
C1 e C2 é alcançável a partir de qualquer outro, pois
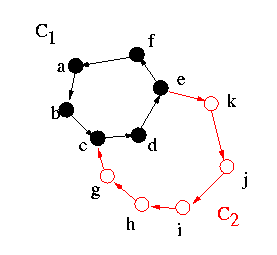
existe um caminho fechado que passa por todos os vértices. Por exemplo, na
figura 15, temos o caminho fechado a, b, c, d, e, k, j, i, h, g, c, d, e, f, a.
Continuando assim até que todos os vértices do grafo sejam considerados,
obteremos um grafo que contém um caminho fechado passando por todos os vérties,
pois ele é conexo. As arestas que sobram, depois desse processo, podem ter
qualquer orientação.
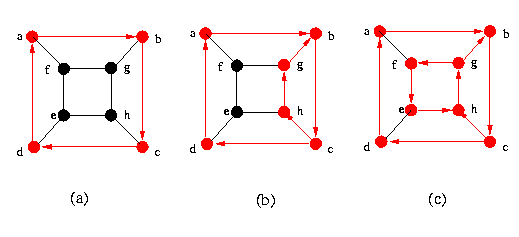
Figura 15 A prova do teorema 1-7 pode ser aproveitada para identificar o algoritmo que
transmorma um grafo não direcionado em um grafo direcionado fortemente conexe.
Considere por exemplo o grafo da figura 5. Como ele não contém nenhuma ponte,
ele pode ser transformado em grafo direcionado fortemente conexo. Primeiro
podemos orientar o ciclo a-b-c-d-a, como ilustrado na figura 16a. Depois podemos
acrescentar o ciclo c-h-g-b-c (veja o resultado na figura 16b). Depois dessa
etapa sobram os dois vértices e e f. Na figura 16c, podemos ver que o acréscimo
do ciclo g-f-e-h-g termina o processo. Agora todos os vértices fazem parte de um
caminho fechado: a-b-c-h-g-f-e-h-g-b-c-d-a. As arestas que sobram podem ter
qualquer orientação. As figura 17 ilustra um resultado final possível.
Figura 16 Figura 17 Uma consequência importante do teorema 1-7 é o seguinte teorema:
Teorema 1-8: O grafo subjacente de um grafo fortemente conexo não
pode conter uma ponte.
A demonstração do teorema 1-7 sugere também um outro teorema:
Teorema 1-9: Um grafo é fortemente conexo se e somente se existe um
caminho fechado que passa por todos os vértices do grafo.
Ida: Suponhamos G um grafo fortemente conexo, e u,v dois
vértices desse grafo. Existe um caminho de u para v e de v
para u. Então, existe um caminho fechado que contém u e v.
Suponhamos agora um outro vértice w. Existe um caminho de u para
w e de w para u. Isso implica que existe também um caminho
fechado que contém os três vértices u v e w (veja figura
18). Continuando assim com os outros vértices do grafos, obteremos um caminho
fechado que passa por todos os vértices do grafo.
Volta: Trivial. Eu deixo como exercício.
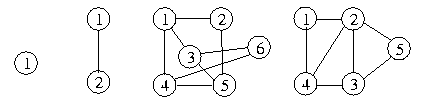
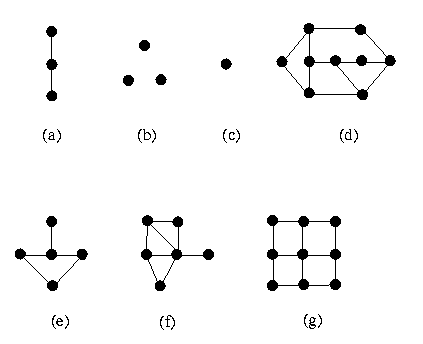
Figura 18 Exercício 1-1: Desenhe todos of grafos simples que é possível
construir com 1, 2, 3, e 4 vértices.
Exercício 1-2: O complemento de um grafo simples G = (V,E) é o grafo
simples G- = (V,F), no qual existe uma aresta entre dois vértices se
e somente se não existe uma aresta entre os mesmos vertices em G. Desenhe o
complemento dos seguintes grafos:
Figura 19 Exercício 1-3: Mostre que o complemento de um grafo bipartite não é
necessariamente um grafo bipartite.
Exercício 1-4: Mostre que G U G- é um grafo completo.
Exercício 1-5: Utilize o teorema 1-1 para provar que 1 + 2 + ... +
(n-1) = n(n-1)/2.
Exercício 1-6: Seja G um grafo com v vértices e a
arestas. Quantas arestas contém o grafo G-?
*Exercício 1-7: Provar: se G é um grafo que contém 6 vértices, G ou
G- (possivelmente ambos) deve conter um grafo isomorfo a
K3.
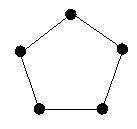
Exercício 1-8: Provar que se G é um grafo cíclico de 5 vértices (ver
figura 20), ele é isomorfo a G-.
Figura 20 Exercício 1-9: Seja v o número de vértices em um grafo G.
Provar que se G é isomorfo a G-, um dos dois valores v e
v-1 é múltiplo de 4.
Exercício 1-10: Mostre que não existe um grafo simples que contém 12
vértices e 28 arestas e no qual: Exercício 1-11: Mostre que o número de vértices em um grafo regular de
grau k é par se k é ímpar.
Exercício 1-12: Mostre que não é possível ter um grupo de 7 pessoas,
no qual cada um conhece exatamente 3 outras pessoas.
Exercício 1-13: Mostre que se um grafo bipartite é regular, os dois
subgrafos X e Y que o compõem têm o mesmo número de arestas e o mesmo número de
vértices.
Exercício 1-14: Um grafo cúbico é um grafo simples regular de grau 3.
Construa 2 grafos cúbicos não-isomorfos.
Exercício 1-15: Qual é o número máximo de arestas em um grafo
bipartite?
Exercício 1-16: Mostre que o grafo da figura 7a é isomorfo ao grafo da
figura 7c, redesenhando-o passo a passo.
Exercício 1-17: Mostre que os grafos da figura 21 são isomorfos.
Figura 21 Exercício 1-18: Prove que quaisquer dois grafos conexos com n
vértices, todos de grau 2, são isomorfos.
*Exercício 1-19: Prove que um grafo simples que contém n
vértices é necessariamente conexo se ele tem mais de (n-1)(n-2)/2 arestas.
Exercício 1-20: Desenhe um grafo conexo que fica desconexo quando
qualquer uma das sua arestas é retirada.
Exercício 1-21: Prove que um grafo de n vértices satisfazendo a
condição do exercício 1-20 Exercício 1-22: Mostre que dois grafos simples são isomorfos se e
somente se o seus complementos são isomorfos.
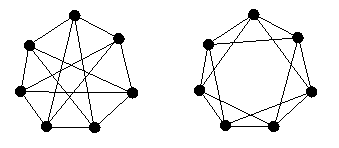
Exercício 1-23: Quais dos grafos da figura 22 são isomorfos? (Tente
com cada uma das técnicas explicada nessa apostila)
Figura 22 Exercício 1-24: Mostre que se num grupo de pessoas, existem no mínimo
duas pessoas que não se conhecem, é possível formar um subgrupo desse grupo tal
que nele não existem duas pessoas que se conhecem e que toda pessoa não incluida
nesse subgrupo conhece no mínimo uma pessoa do subgrupo.
Exercício 1-25: Prove que um grafo conexo continua conexo depois da
remoção de uma aresta ai se e somente se ai faz parte de
um ciclo.
Exercício 1-26: Para cada grafo da figura 23, indique se ele é
bipartite. Caso ele é, redesenhe o grafo de maneira a distinguir os dois
subconjuntos de vértices.
Figura 23 Exercício 1-27: Mostre que não existe um conjunto independente de 3
vértices no grafo ilustrado na figura 9.
Exercício 1-28: Considere o grafo da figura 6a. É possível
transformá-lo em grafo fortemente conexo? Se for, inspire-se da prova do teorema
1-7 para transformá-lo em grafo fortemente conexo.
Exercício 1-29: Um torneio é um grafo direcionado cujo grafo
subjacente é um grafo completo. Prove que nesse tipo de grafo não pode existir
mais de um vértice de grau de entrada nulo e mais de um vértice de grau de saída
nulo.
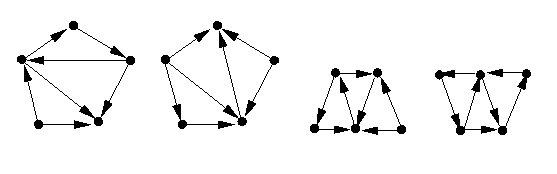
Exercício 1-30: Considere a figura 24. Quais desses grafos são
isomorfos.
Figura 24 Exercício 1-31: Seja G um grafo direcionado simples de n
vértices e a arestas.
Exercício 1-31: Prove a volta do Teorema 1-3.
Exercício 1-32: Sejam G1 e G2 dois grafos
simples de n vértices. Suponha também que nesses grafos nenhum vértice
possui grau superior a 2. Proponha um algoritmo em O(n) para determinar
se esses grafos são isomorfos.
Exercício 1-33: Prove que se um grafo conexo G é decomposto em dois
subgrafos g1 e g2, existe necessariamente um vértice comum
entre g1 e g2.
Exercício 1-34: Mostre que a união de dois caminhos disjuntos (que não
tem aresta em comum) entre dois vértices resulta em um circuito. Exercício 1-35: Seja um grafo simples de n vértices tal que por
qualquer par de vertices distintos vj e vk, temos:
d(vj) + d(vk) Exercício 1-36: Desenhe G1 U G2 nos três casos
ilustrados na figura 25.
Figura 25 Exercício 1-37: Determine quais desses vetores de grau são gráficos:
Exercício 1-38: Oriente as arestas dos grafos das figuras 6a, 7, 13,
23d e 23g para obter um grafmo fortemento conexo.
Exercício 1-39: Mostre que qualquer vetor de grau deve conter no
mínimo dois valores iguais.
Exercício 1-40: Mostre que um vetor de grau corresponde a um
multigrafo se e somente se a soma dos valores desse vetor é par.
Exercício 1-41: Suponhamos que ninguem tem mais de 2.000.000 de
cabelos. Utilize a teoria dos grafos para mostrar que deve existir na cidade de
São Paulo no mínimo duas pessos que tem exatamente o mesmo número de cabelos.
Exercício 1-42: Moste que qualquer subgrafo de um grafo bipartite é um
grafo bipartite.
Vetor de grau
Subgrafos
 V1 e E2
V1 e E2  E1. Podemos verificar facilemente
os seguintes enunciados:
E1. Podemos verificar facilemente
os seguintes enunciados:
Eis alguns subgrafos interessantes:
Caminho
 i < n-1. Essa
seqüência é dita um caminho de v1 a vn. Um caminho
que não passa duas vezes pelo mesmo vértice é um caminho simples (ou
elementar). Um caminho que não contém duas vezes a mesma aresta é um
trajeto. Note que essa definição de caminho funciona realmente somente
com grafo simples.
i < n-1. Essa
seqüência é dita um caminho de v1 a vn. Um caminho
que não passa duas vezes pelo mesmo vértice é um caminho simples (ou
elementar). Um caminho que não contém duas vezes a mesma aresta é um
trajeto. Note que essa definição de caminho funciona realmente somente
com grafo simples.
Grafo conexo
Um grafo G = (V,E) é conexo quando existe um caminho entre
cada par de V. Caso contrário o grafo é desconexo. Um grafo é
totalmente desconexo quando não existe nenhuma aresta. A representação
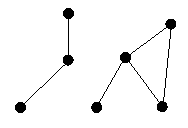
gráfica dum grafo desconexa contém no mínimo dois "pedaços". A figura 12 ilustra
um grafo desconexo. Cada "pedaço" de um grafo é chamado componente
conexo. O grafo da figura 12 tem 2 componentes conexos.
Grafo bipartite
Grafo direcionado
Um grafo G = (V,E) é um conjunto não-vazio V, cujos
elementos são chamados vértices, e um conjunto E de arestas. Uma
aresta é um par ordenado (vj,vk). Diz-e que cada aresta
(vj,vk) possui uma única direção de vj para
vk. Também a aresta (vj,vk) e dita
divergente de vj e convergente a vk. O
número de arestas divergentes e convergentes de um vértice são chamados grau
de saída e grau de entrada, respectivamente. A figura 14 ilustra um
exemplo de grafo direcionado.
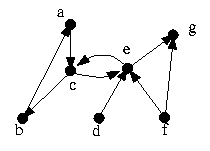
E =
{(a,c),(c,b),(b,a),(c,e),(e,c),(d,e),(e,g),(f,g),(f,e)}
Exercícios
b) O grau de cada vértice é 3 ou
6.
b) contém exatamente n-1 arestas.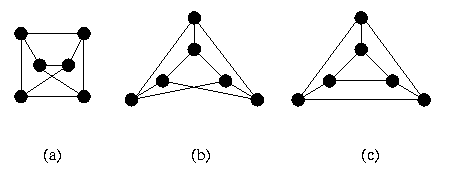
 a
a  n(n - 1).
n(n - 1).
b) Quais são os limites inferior e superior para a
se G é fortemente conexo?  n-1.
Prove que esse grafo é necessariamente conexo.
n-1.
Prove que esse grafo é necessariamente conexo.
Atualizada por Milton Procópio de Borba