Três canibais e três missionários estão viajando juntos e chegam à margem de um rio. Eles desejam atravessar para a outra margem para, desta forma, continuar a viagem. O único meio de transporte disponível é um barco que comporta no máximo duas pessoas. Há uma outra dificuldade: em nenhum momento o número de canibais pode ser superior ao número de missionários pois desta forma os missionários estariam em grande perigo de vida. Como administrar a travessia?
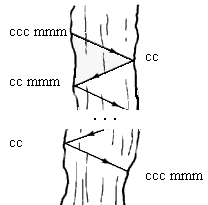Para resolver este problema, considere as situações (ou estados) no
que se refere ao número de canibais e missionários que estão numa das duas
margens, sempre considerando que o barco está aportado, ou seja, antes do
início de uma travessia ou quando ela foi completada. Podemos representar cada
um destes estados por uma tripla de valores (c,m,b), onde c e
m representam o número de canibais e de missionários, respectivamente,
que estão na margem b onde está o barco.
Uma tripla como (2, 2, esquerda) significa que temos dois canibais e dois missionários na margem esquerda, e que o barco está nesta margem. Apesar de não estar explicitamente dito, é fácil saber que neste instante temos 1 canibal e 1 missionário na margem direita (complemento em relação ao par (3,3)).
Um modelo para este problema é dado, então, pelo grafo G(V,A):
V = { (c,m,b) | c e m representam o número de canibais e de missionários na margem b do rio, estando o barco nesta margem}
A = { (ex,ey) | ex = (cx,mx,bx) é o estado na margem onde o barco está antes da travessia ser iniciada, e ey = (cy,my,by) é o estado na margem oposta após o barco completar a travessia}
Como o barco comporta no máximo 2 pessoas, há 5 possíveis situações quanto aos passageiros do barco em cada travessia:
A tabela que se segue descreve as restrições par que uma travessia possa ocorrer, considerando x e y com sendo as margens de origem e de destino de uma travessia do barco, respectivamente.
| regra | pré-condição | ação | pós-condição |
| 1 | cx ³ t (3 - mx) = 0 ou (3 - mx) - (3 - cx) ³ t 1 £ t £ 2 |
travessia de t canibais da margem x para y | cy = (3 - cx) + t my = (3 - mx) |
| 2 | mx ³ t mx - t = 0 ou (mx - t) ³ cx (3 - cx) = 0 ou (3 - cx) - (3 - mx) £ t 1 £ t £ 2 |
travessia de t missionários da margem x para y | my = (3 - mx) + t cy = (3 - cx) |
| 3 | cx ³ 1 mx ³ 1 (3 - cx) = 0 ou (3 - cx) £ (3 - mx) |
travessia de 1 canibal e de 1 missionário da margem x para y | cy = (3 - cx) +
1 my = (3 - mx) + 1 |
Regra 1
Para que t canibais, 1 £ t £ 2, atravessem sozinhos o rio, é preciso que haja t canibais na margem de origem (cx ³ t). Também é preciso que ao chegarem estes t canibais na margem de destino, o número total de canibais não exceda o número de missionários. Isto é obtido em duas situações: se não houver nenhum missionário na margem oposta antes da travessia do barco, ou seja, (3 - mx) = 0; haja pelo menos t missionários a mais do que canibais na margem oposta antes da travessia do barco, ou seja, (3 - mx ) - (3 - cx) ³ t.
Regra 2
Para que t missionários, 1 £ t £ 2, atravessem sozinhos o rio, é preciso que haja t missionários na margem de origem (mx ³ t). Também é preciso que não restem mais canibais do que missionários na margem de origem, ou seja, que (mx - t) ³ cx, ou que o número de missionários restantes seja zero (mx - t = 0). Quanto à margem de destino, ou ela não tem nenhum canibal antes do início da travessia (3 - cx) = 0, ou o número de canibais não exceda o número de missionários em mais do que t unidades ((3 - cx) - (3 - mx) £ t).
Regra 3
Para que 1 canibal e 1 missionário atravessem o rio, é preciso que haja pelo menos 1 canibal (cx ³ 1) e 1 missionário (mx ³ 1) na margem de origem. Também é preciso garantir que o número de canibais não exceda o número de missionários na margem de destino, ou seja, que não haja nenhum canibal antes da travessia ((3 - cx) = 0), ou que o número de canibais não seja superior ao número de missionários ((3 - cx) £ (3 - mx)).
Um algoritmo de busca em profundidade que implementa estas regras é dado na tabela que se segue:
grafo := Grafo new. self buscaEmProfundidadeDe: #(3 3 esquerda) para: #(3 3 direita) jaVisitados: Set new. |
buscaEmProfundidadeDe: origem para: destino jaVisitados: visitados |cx mx cy my| origem = destino ifTrue: [ ^self ]. visitados add: origem. cx := origem at: 1. mx := origem at: 2. cy := 3 - cx. my := 3 - mx. 1 to: 2 do: [:t| (cx >= t and: [my = 0 or: [my - cy >= t]]) ifTrue: [ self travessiaDeCanibais: t de: origem para: destino jaVisitados: visitados ]. (mx >= t and: [(mx - t = 0) | (mx - t >= cx) and: [(cy = 0) | (cy - my <= t)]]) ifTrue: [ self travessiaDeMissionarios: t de: origem para: destino jaVisitados: visitados ]. ]. (cx >= 1 and: [mx >= 1 and: [(cy = 0) | (cy <= my)]]) ifTrue: [ self travessiaDeUmCanibalUmMissionarioDe: origem para: destino jaVisitados: visitados ] |
travessiaDeCanibais: t de: origem para: destino
jaVisitados: visitados
|cx mx cy my meio margemDoBarco|
cx := origem at: 1.
mx := origem at: 2.
cy := 3 - cx.
my := 3 - mx.
meio := origem copy.
meio at: 1 put: cy + t.
meio at: 2 put: my.
(origem at: 3) = #direita ifTrue: [
meio at: 3 put: #esquerda
] ifFalse: [
meio at: 3 put: #direita
].
grafo conecta: origem a: meio rotulo: (Array with: t with: 0).
(visitados includes: meio) ifFalse: [
self buscaEmProfundidadeDe: meio para: destino
jaVisitados: visitados.
]
|
travessiaDeMissionarios: t de: origem para: destino
jaVisitados: visitados
|cx mx cy my meio margemDoBarco|
cx := origem at: 1.
mx := origem at: 2.
cy := 3 - cx.
my := 3 - mx.
meio := origem copy.
meio at: 1 put: cy.
meio at: 2 put: my + t.
(origem at: 3) = #direita ifTrue: [
meio at: 3 put: #esquerda
] ifFalse: [
meio at: 3 put: #direita
].
grafo conecta: origem a: meio rotulo: (Array with: 0 with: t).
(visitados includes: meio) ifFalse: [
self buscaEmProfundidadeDe: meio para: destino
jaVisitados: visitados.
]
|
travessiaDeUmCanibalUmMissionarioDe: origem para: destino
jaVisitados: visitados
|cx mx cy my meio margemDoBarco|
cx := origem at: 1.
mx := origem at: 2.
cy := 3 - cx.
my := 3 - mx.
meio := origem copy.
meio at: 1 put: cy + 1.
meio at: 2 put: my + 1.
(origem at: 3) = #direita ifTrue: [
meio at: 3 put: #esquerda
] ifFalse: [
meio at: 3 put: #direita
].
grafo conecta: origem a: meio rotulo: (Array with: 1 with: 1).
(visitados includes: meio) ifFalse: [
self buscaEmProfundidadeDe: meio para: destino
jaVisitados: visitados.
]
|
O grafo obtido por este algoritmo é apresentado abaixo:
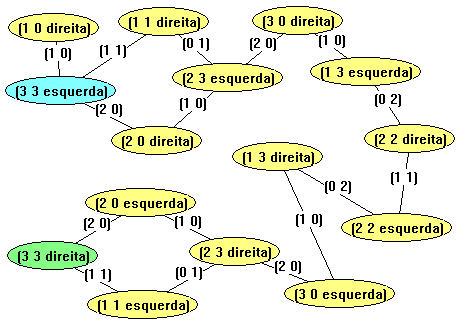
Por este grafo é possível observar que há quatro possíveis seqüências de travessias para efetuar o translado dos canibais e dos missionários e que em todas elas são necessárias no mínimo 11 travessias do barco .