 Considere o jogo de xadrez. Seguindo as regras
de movimento do cavalo, é possível que um cavalo parta de uma casa
qualquer, percorra todo o tabuleiro visitando cada casa uma e somente uma
única vez e retorne à casa inicial?
Considere o jogo de xadrez. Seguindo as regras
de movimento do cavalo, é possível que um cavalo parta de uma casa
qualquer, percorra todo o tabuleiro visitando cada casa uma e somente uma
única vez e retorne à casa inicial?
 Considere o jogo de xadrez. Seguindo as regras
de movimento do cavalo, é possível que um cavalo parta de uma casa
qualquer, percorra todo o tabuleiro visitando cada casa uma e somente uma
única vez e retorne à casa inicial?
Considere o jogo de xadrez. Seguindo as regras
de movimento do cavalo, é possível que um cavalo parta de uma casa
qualquer, percorra todo o tabuleiro visitando cada casa uma e somente uma
única vez e retorne à casa inicial?
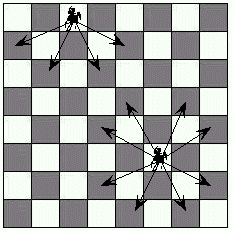
No xadrez o movimento o cavalo é sempre em L (letra ele), ou seja, duas casas num sentido (vertical ou horizontal) e uma casa no outro sentido (horizontal ou vertical). Na figura ao lado estão postos dois cavalos, sendo que cada uma das setas indica um dos possíveis movimentos dos cavalos.
Um modelo para este problema é definir o grafo G(V,A) como:
V = { c| c é uma casa do tabuleiro de xadrez}
A = { (c1,c2) | a casa c2 pode ser atingida a partir da casa c1 por um único movimento de cavalo}
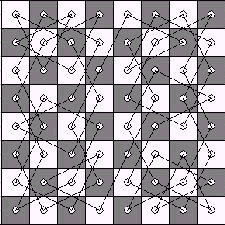
A solução deste problema passa por verificar se o grafo G é hamiltoniano. Este grafo tem 64 vértices e 168 arestas, e, em realidade, contém vários ciclos hamiltonianos, um os quais é apresentado na figura que se segue.
 Neste problema, a definição do grafo G(V,A) pode ser bem mais
direcionada para um possível implementação computacional se introduzirmos um
pouco mais de formalismo quando da definição dos vértices e das arestas.
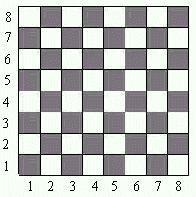
Considere que tenhamos enumerado as linhas e colunas do tabuleiro de 1 a 8,
conforme figura ao lado. O grafo poderia ser, entãio definido por:
Neste problema, a definição do grafo G(V,A) pode ser bem mais
direcionada para um possível implementação computacional se introduzirmos um
pouco mais de formalismo quando da definição dos vértices e das arestas.
Considere que tenhamos enumerado as linhas e colunas do tabuleiro de 1 a 8,
conforme figura ao lado. O grafo poderia ser, entãio definido por:
V = { (l,c) | l e c são a linha e a coluna, respectivamente, que denotam uma casa do tabuleiro de xadrez}
A = { (v1,v2) | a casa v2 = (l2,c2) pode ser atingida a partir da casa v1 = (l1,c1) por um único movimento de cavalo, ou seja,
| l1 - l2 | + | c1 - c2| = 3,
l1 ~= l2,
c1 ~= c2 }
Temos, agora, um critério matemático simples que permite identificar as 64 casas do tabuleiro e todas os possíveis movimentos de um cavalo (168 arestas).