Fluxo em REDES

Uma rede é um grafo dirigido e sem laços que possui exatamente uma raiz e uma anti-raiz.

Associando a cada aresta a da rede um valor c(a) que corresponde à capacidade da aresta, podemos definir uma função Ø(a) que correspondente ao fluxo da aresta. Esta função satisfaz as seguinte restrições:

Fluxo Ø :

1. Ø(a) ³ 0 - fluxo é não negativo em cada arco
2. Ø(a) £ c(a) - fluxo não excede a capacidade do arco
3. O fluxo que entra é o mesmo que sai de um vértice
4. O fluxo que entra na fonte (raiz) é o mesmo que chega ao sumidouro (anti-raiz), que é o fluxo máximo Ø₀ da rede

O objetivo é obter o fluxo máximo Ø₀ da rede

Algoritmo de FORD-FULKERSON

1. Introduz-se um fluxo arbitrário compatível (fluxo de cada arco não exceda a capacidade)
2. Obtém-se um fluxo completo (todos os caminhos contenham pelo menos um arco saturado)
3. Obtém-se o fluxo máximo
   • 3.1.Marca-se a fonte com sinal +
   • 3.2.Um vértice Xi estando marcado:
     • a) marcar com + Xi todo vértice Xj não marcado tal que existe um arco (Xi,Xj) não saturado
     • b) marcar com - Xi todo vértice Xj não marcado tal que exista um arco (Xj, Xi) percorrido por um fluxo não nulo
   • 3.3. Se o fluxo não for máximo, considera-se a seqüência de vértices marcados (+ ou -) indo da fonte ao sumidouro; se um arco desta seqüência é orientado no sentido da seqüência soma-se, em caso contrário subtrai-se uma unidade ao fluxo desse arco;
   • 3.4.Apaga-se as marcas e retorna-se ao passo 3.1 até que não seja possível marcar o sumidouro (passo 3.3)

Uma Rede:

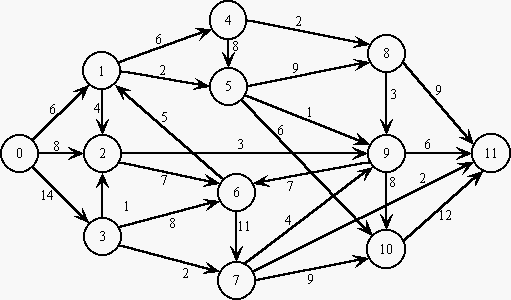
Após a introdução de um fluxo arbitrário compatível (passo 1):

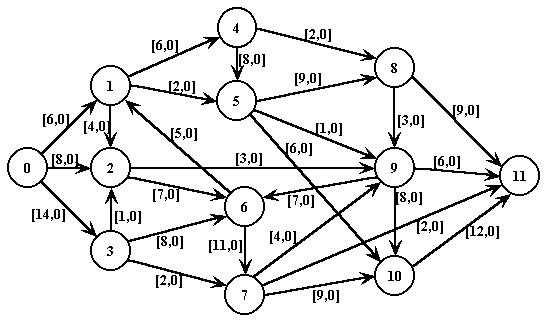
Após computo do fluxo completo (todos os caminhos contenham pelo menos um arco saturado)  (passo 2):

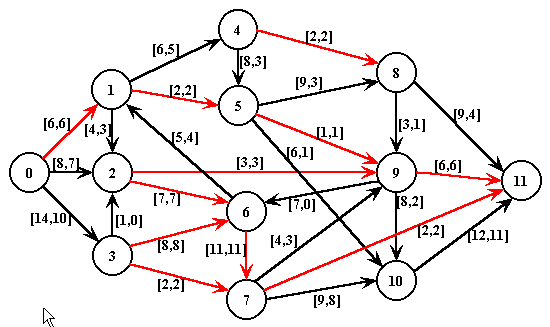
Após marcações (passos 3.1 e 3.2)

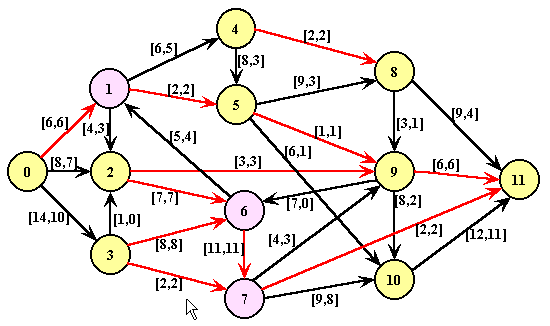
Cômputo da seqüência do caminho que pode ser otimizado (passos 3.3)

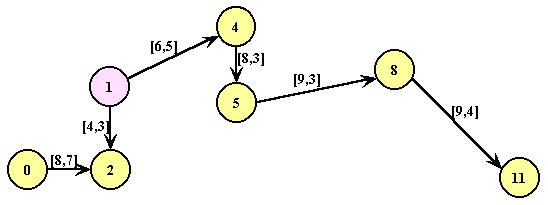
Rede após otimização do caminho anterior (passo 3.3):

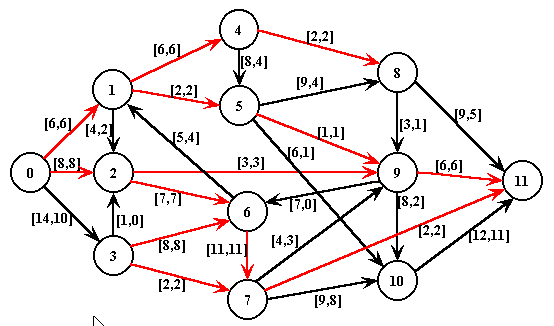
Rede após nova tentativa de marcação (passos 3.4, 3.1 e 3.2):

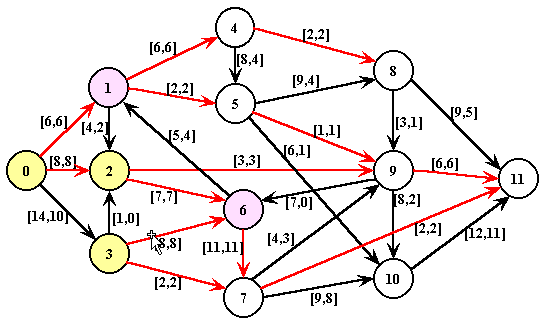
Como a antri-raiz não foi marcada, o fluxo nesta rede é maximo.