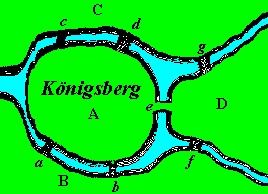

No século 18 havia na cidade de Königsberg um conjunto de sete pontes (identificadas pelas letras de a até f na figura ao lado ) que cruzavam o rio Pregel . Elas conectavam duas ilhas (A e D) entre si e as ilhas com as margens (B e C).
Por muito tempo os habitantes daquela cidade perguntavam-se se era possível cruzar as sete pontes numa caminhada contínua sem que se passasse duas vezes por qualquer uma delas.
Este problema pode ser representado por um multigrafo G(V,A), tal que:
V = { m | m é uma ilha ou uma margem }
A = { (m1,m2, p) | as margens ou ilhas m1 e m2 são ligados pela ponte p }
cuja representação gráfica pode ser vista na figura ao lado.
Modelado
desta forma, o Problema das Pontes de Königsberg é essencialmente um problema de
determinar se o multigrafo correspondente possue uma trilha (possivelmente um
ciclo) euleriana. Como os graus de todos os vértices são impares, é fácil
verificar que este grafo não apresenta nem uma trilha, nem um ciclo euleriano,
visto que ele não satisfaz o teorema de Euler, nem tampouco é um grafo atravessável. Logo, a travessia proposta não é possível.
Ver também grafos hamiltonianos com outras aplicações.