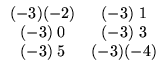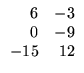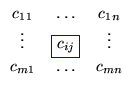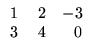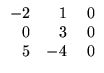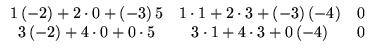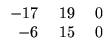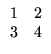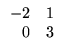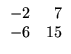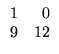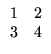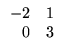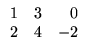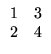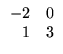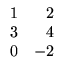Matrizes
Operando com matrizes estamos utilizando uma forma compacta de fazermos operações com vários números simultaneamente.
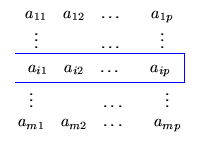
Definição. Uma matriz A,
m x n (m por n), é uma tabela de mn
números dispostos em m linhas e n colunas
A i-ésima linha
de A é
para i = 1,..., m e a
j-ésima coluna de A é
para j = 1,..., n. Usamos
também a notação A =
(aij)m x n. Dizemos que
aij ou [A]ij é o elemento ou a
entrada de posição i j da matriz A. Se m = n, dizemos que A é uma matriz
quadrada de ordem n. Dizemos que a11,
a22,..., ann formam a diagonal
(principal) de A.
Exemplo. Considere as seguintes
matrizes:
As matrizes A e B são 2 x 2. A matriz C é 2
x 3, D é 1 x 3, E é 3 x 1 e F é
1 x 1. De acordo com a notação que introduzimos, exemplos de elementos
de algumas das matrizes dadas acima são
a12 = 2,
c23 = - 2, e21 = 4, [A]22 = 4, [D]12 = 3.
Vamos, agora, introduzir as operações matriciais.
Definição. A soma de duas
matrizes de mesmo tamanho A
= (aij)m x n e B = (bij)m
x n é definida como sendo a matriz
C = (cij)m
x n obtida somando-se os elementos correspondentes de A e
B, ou seja,
cij = aij +
bij ,
para i = 1,..., m e j = 1,..., n. Escrevemos C =
A + B e [A +
B]ij = aij + bij.
Exemplo. Considere as matrizes:
Se chamamos de C a soma das duas matrizes A e B,
então
Definição. A multiplicação de uma
matriz A =
(aij)m x n por um escalar (número)
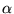 é definida pela matriz B = (bij)m
x n obtida multiplicando-se cada elemento da matriz pelo escalar,
ou seja,
é definida pela matriz B = (bij)m
x n obtida multiplicando-se cada elemento da matriz pelo escalar,
ou seja,
bij =
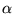 aij
aij ,
para i = 1,..., m e j = 1,..., n. Escrevemos B = 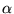 A e [
A e [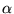 A]ij =
A]ij = 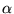 aij.
aij.
Exemplo. O produto da matriz A = 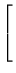
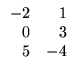
![$ \left.\vphantom{\begin{array}{rr}
-2&\;1\\
0&3\\
5&-4
\end{array}}\right]$](Mais_matriz_files/s1img48.gif) pelo
escalar -3 é dado por
pelo
escalar -3 é dado por
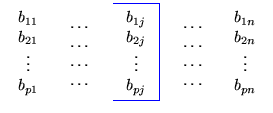
Definição. O produto de duas
matrizes, tais que o número de colunas da primeira matriz é igual ao número
de linhas da segunda, A =
(aij)m x p e B = (bij)p
x n é definido pela matriz C = (cij)m
x n obtida da seguinte forma:
| cij |
= |
ai1b1j +
ai2b2j +...+
aipbpj |
(1) |
| |
= |
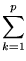 aikbkj , aikbkj , |
(2) |
para i = 1,..., m e j = 1,..., n. Escrevemos C =
AB e
[AB]ij
= 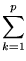 aikbkj.
aikbkj.
A equação (1) está dizendo que o elemento i j do produto é igual a soma dos
produtos dos elementos da i-ésima linha de A pelos elementos
correspondentes da j-ésima coluna de B.
Na equação (2) estamos
usando a notação de somatório para escrever a equação (1) de
forma compacta.
O símbolo 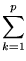 significa
que estamos fazendo uma soma em que o índice k está variando de k
= 1 até k = p.
significa
que estamos fazendo uma soma em que o índice k está variando de k
= 1 até k = p.
Exemplo. Considere as matrizes:
Se chamamos de C o produto das duas matrizes A e B,
então
Observe que neste exemplo o produto BA não está definido.
Entretanto, mesmo quando está definido, BA pode não ser igual a
AB, como mostra o exemplo seguinte.
Exemplo.
Sejam
Então
Definição. A transposta de uma
matriz A =
(aij)m x n é definida pela matriz B = (bij)n
x m obtida trocando-se as linhas pelas colunas, ou seja,
bij = aji ,
para i = 1,..., m e j = 1,..., n. Escrevemos B =
At e
[At]ij =
aji.
Exemplo. As transpostas das matrizes
são
Ver também: Propriedades das Operações Matriciais
Parte da página construída por Reginaldo de Jesus Santos
Atualizada por Milton Procópio de Borba


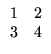
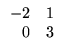
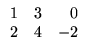
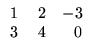
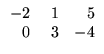
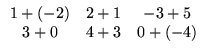
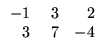
![]() é definida pela matriz B = (bij)m
x n obtida multiplicando-se cada elemento da matriz pelo escalar,
ou seja,
é definida pela matriz B = (bij)m
x n obtida multiplicando-se cada elemento da matriz pelo escalar,
ou seja,
![]()
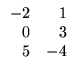
![]() pelo
escalar -3 é dado por
pelo
escalar -3 é dado por