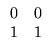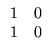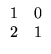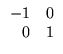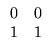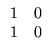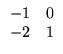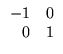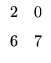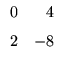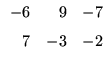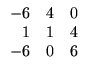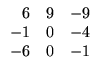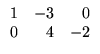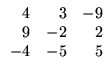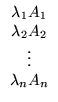A seguir, mostraremos as propriedades que
são válidas para a aritmética matricial. Elas são muito semelhantes àquelas que
são válidas para os números reais. Uma propriedade importante que é válida para
os números reais, mas não é válida para as matrizes é a comutatividade do
produto, como foi mostrado num
Exemplo.
Por ser compacta, usaremos a notação de somatório na demonstração de várias
propriedades.
Teorema.
Sejam A, B e C matrizes com tamanhos apropriados,  e
e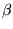 escalares. São válidas as seguintes propriedades para as
operações matriciais:
escalares. São válidas as seguintes propriedades para as
operações matriciais:
- 1. A + B = B + A;
- 2. A + ( B + C ) = ( A + B ) + C;
- 3. Existe uma única matriz
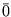 m x n, tal que A +
m x n, tal que A + 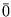 = A , para qualquer matriz A, m x n.
= A , para qualquer matriz A, m x n.
A matriz 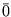 é chamada matriz nula.
é chamada matriz nula.
- 4. Para cada matriz A, existe uma única matriz B, tal que A + B =
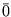 . Representamos B por - A.
. Representamos B por - A.
- 5.
 (
(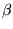 A) = (
A) = (
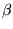 )A;
)A;
- 6. (
 +
+ 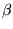 )A =
)A =  A +
A + 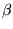 A;
A;
- 7.
 (A + B) =
(A + B) =  A +
A +  B;
B;
- 8. A(BC) = (AB)C;
- 9. A(B + C) = AB +
AC e (A + B)C =
AC + BC;
- 10.
 (AB) = (
(AB) = ( A)B = A(
A)B = A( B);
B);
- 11. (At)t = A;
- 12. (A + B)t =
At + Bt;
- 13. (AB)t =
BtAt;
- 14. (
 A)t =
A)t =  At;
At;
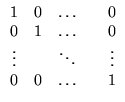
- 15. A matriz, n x n,
chamada matriz identidade é tal que
A In =
A, para qualquer
matriz A = (aij)m
x n e
In B =
B, para qualquer
matriz B = (bij)n
x m.
Demonstração. Para provar as igualdades
acima, devemos mostrar que os elementos da matriz do lado esquerdo são iguais
aos elementos correspondentes da matriz do lado direito. Serão usadas várias
propriedades dos números sem citá-las explicitamente.
- 1.
- (A
+ B)ij = aij + bij =
bij + aij = (B +
A)ij;
- 2.
- [A
+ (B + C)]ij = aij + (B +
C)ij = aij + (bij +
cij) = (aij + bij) +
cij = (A + B)ij +
cij = [(A + B) + C]ij;
- 3.
- Seja U uma matriz m x n tal que
para qualquer matriz A, m x n. Comparando os
elementos correspondentes, temos que
aij + uij =
aij ,
ou seja, uij = 0, para
i = 1..., m e j = 1..., n. Portanto, a única
matriz que satisfaz à equação acima é a matriz em que todos os seus elementos são iguais a zero. Denotamos esta matriz
por 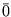 .
.
- 4.
- Dada uma matriz A, m x n, seja B uma
matriz m x n, tal que
A + B = 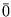 . . |
Comparando os elementos correspondentes, temos que
aij + bij = 0 ,
ou seja, bij = -
aij, para i = 1...,
m e j = 1..., n. Portanto, a
única matriz que satisfaz 'a equação acima é a matriz em que todos os seus elementos são iguais aos simétricos dos elementos
de A. Denotamos esta matriz por - A.
- 5.
- [
 (
(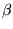 A)]ij =
A)]ij =  (
(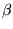 aij) = (
aij) = (
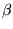 )aij = [(
)aij = [(
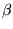 )A]ij.
)A]ij.
- 6.
- [(
 +
+ 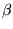 )A]ij = (
)A]ij = ( +
+ 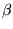 )aij = (
)aij = ( aij) + (
aij) + (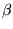 aij) = [
aij) = [ A]ij + [
A]ij + [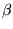 A]ij = [
A]ij = [ A +
A + 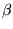 A]ij.
A]ij.
- 7.
- [
 (A + B)]ij =
(A + B)]ij =  (aij + bij)
=
(aij + bij)
=  aij +
aij +  bij = [
bij = [ A]ij + [
A]ij + [ B]ij = [
B]ij = [ A +
A +  B]ij.
B]ij.
- 8.
- A demonstração deste item é a mais trabalhosa. Sejam A, B e
C matrizes m x p, p x q e
q x n respectivamente. A notação de somatório aqui pode
ser muito útil, pelo fato de ser compacta.
| [A(BC)]ij |
= |
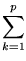 aik(BC)kj = aik(BC)kj =
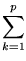 aik( aik(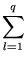 bklclj) = bklclj) = 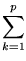 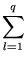 aik(bklclj)
= aik(bklclj)
= |
|
| |
= |
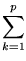 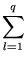 (aikbkl)clj
= (aikbkl)clj
= 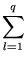 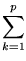 (aikbkl)clj
= (aikbkl)clj
= 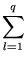 ( (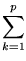 aikbkl)clj
= aikbkl)clj
= |
|
| |
= |
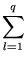 (AB)ilclj =
[(AB)C]ij . (AB)ilclj =
[(AB)C]ij . |
|
- 9.
- Usando a notação do Somatório,
| [A(B + C)]ij |
= |
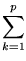 aik(B +
C)kj = aik(B +
C)kj = 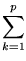 aik(bkj +
ckj) = aik(bkj +
ckj) = 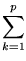 (aikbkj +
aikckj) = (aikbkj +
aikckj) = |
|
| |
= |
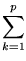 aikbkj + aikbkj + 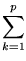 aikckj =
(AB)ij + (AC)ij = [AB +
AC]ij . aikckj =
(AB)ij + (AC)ij = [AB +
AC]ij . |
|
A outra igualdade é inteiramente análoga a anterior e deixamos como
exercício.
- 10.
- [
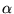 (AB)]ij =
(AB)]ij = 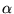
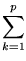 aikbkj =
aikbkj = 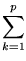 (
(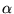 aik)bkj = [(
aik)bkj = [(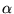 A)B]ij
A)B]ij
e
[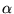 (AB)]ij =
(AB)]ij = 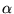
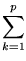 aikbkj =
aikbkj = 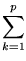 aik(
aik(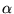 bkj) = [A(
bkj) = [A(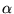 B)]ij.
B)]ij.
- 11.
- [(At)t]ij
= [At]ji = aij.
- 12.
- [(A
+ B)t]ij = [A + B]ji =
aji + bji =
[At]ij + [Bt]ij.
- 13.
- [(AB)t]ij =
[AB]ji =
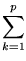 ajkbki =
ajkbki = 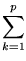 [At]kj[Bt]ik
=
[At]kj[Bt]ik
= 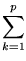 [Bt]ik[At]kj
= = [BtAt]ij.
[Bt]ik[At]kj
= = [BtAt]ij.
- 14.
- [(
 A)t]ij = [
A)t]ij = [ A]ji =
A]ji =  aji =
aji =  [At]ij.
[At]ij.
- 15.
- A demonstração deste item é simples e deixamos como exercício.

A diferença entre duas matrizes de mesmo
tamanho A e B é definida por
A - B = A + (- B),
ou seja, é a soma da matriz A com a simétrica da matriz B.
Exemplo. Vamos verificar se para
matrizes A e B, quadradas, vale a igualdade
| (A + B)(A - B) =
A2 - B2. |
Usando a propriedade (i) do teorema anterior obtemos
| (A + B)(A - B) |
= |
(A + B)A + (A +
B)(- B) |
|
| |
= |
AA + BA - AB - BB =
A2 + BA - AB - B2 |
|
Assim, (A + B)(A
- B) = A2 - B2 se, e somente se,
BA - AB = 0, ou seja, se, e somente se, AB = BA.
Como o produto de matrizes não é comutativo, a conclusão é que a igualdade em questão
não vale para matrizes em geral. Como contra-exemplo basta tomarmos duas
matrizes que não comutem entre si. Sejam
Para estas matrizes
A +
B =
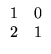
![$\displaystyle \left.\vphantom{
\begin{array}{rr}
1 & 0 \\
2 & 1
\end{array}}\right]$](Pro_matriz_files/s1img105.gif)
,
A -
B =
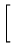
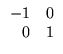
![$\displaystyle \left.\vphantom{\begin{array}{rr}
-1 & 0 \\
0 & 1
\end{array}}\right]$](Pro_matriz_files/s1img108.gif)
,
A2 =
A =
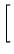
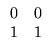
![$\displaystyle \left.\vphantom{
\begin{array}{rr}
0 & 0 \\
1 & 1
\end{array}}\right]$](Pro_matriz_files/s1img99.gif)
,
B2 =
B =
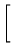
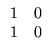
![$\displaystyle \left.\vphantom{
\begin{array}{rr}
1 & 0 \\
1 & 0
\end{array}}\right]$](Pro_matriz_files/s1img102.gif)
.
Assim,
(
A +
B)(
A -
B) =
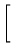
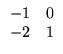
![$\displaystyle \left.\vphantom{
\begin{array}{rr}
-1 & 0 \\
-2 & 1
\end{array}}\right]$](Pro_matriz_files/s1img111.gif)
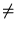
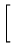
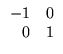
![$\displaystyle \left.\vphantom{\begin{array}{rr}
-1 & 0 \\
0 & 1
\end{array}}\right]$](Pro_matriz_files/s1img108.gif)
=
A2 -
B2.
Exercícios
Numéricos
- 1.
- Considere as seguintes matrizes
Se for possível, calcule:
- (a) AB - BA;
- (b) 2C - D;
- (c) (2Dt -
3Et)t;
- (d) D2 - DE;
2.
Sejam
Verifique que AB =
3A1 + 2A2 + 5A3, onde
Aj é a j-ésima coluna de A, para j = 1,
2, 3.
3.
Encontre um valor de x tal que ABt = 0, onde
4.
Sejam
Encontre:
- (a)
- a 1a. linha de AB;
- (b)
- a 3a. coluna de AB;
- (c)
- a 2a. linha de AtBt;
- (d)
- a 2a. coluna de AtBt.
Exercícios
Teóricos
5. Seja D =
(dij)n x n uma matriz diagonal,
isto é, os elementos que estão fora da diagonal são iguais a zero. Sejam dii = 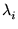 os elementos da diagonal de D.
os elementos da diagonal de D.
- (a)
- Se uma matriz A =
[A1 A2 ...
An], onde Aj é a coluna j
de A, então AD
= [
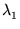 A1
A1 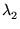 A2 ...
A2 ... 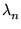 An].
An].
- (b)
- Se uma matriz A =
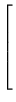
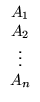
![$ \left.\vphantom{
\begin{array}{c}
A_1\\ A_2\\ \vdots\\ A_n
\end{array}}\right]$](Pro_matriz_files/s1img174.gif) , então DA =
, então DA = 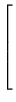
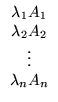
![$ \left.\vphantom{
\begin{array}{c}
\lambda_1A_1\\ \lambda_2A_2\\ \vdots\\ \lambda_nA_n
\end{array}}\right]$](Pro_matriz_files/s1img177.gif) , onde Ai é a linha i de
A.
, onde Ai é a linha i de
A.
- 6.(a) Mostre que a j-ésima coluna do produto AB é igual ao
produto ABj, onde Bj é a j-ésima
coluna de B;
- (b) Mostre que a i-ésima linha do produto AB é igual ao produto AiB, onde Ai é a
i-ésima linha de A.
7. Seja A uma matriz n x
n. Mostre que se AAt =
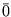 , então A =
, então A = 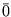 .
8. Se AB = BA e p é um inteiro não negativo, mostre que (AB)p =
ApBp.
9. Sejam A, B e C matrizes n x n.
.
8. Se AB = BA e p é um inteiro não negativo, mostre que (AB)p =
ApBp.
9. Sejam A, B e C matrizes n x n.
- (a)
- (A + B)2 =
A2 + 2AB + B2? E se AB =
BA?
- (b)
- (AB)C = C(AB)? E
se AC = CA e BC = CB?
10. Seja A uma matriz m x n e B
= 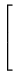
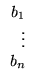
![$ \left.\vphantom{\begin{array}{r}b_1\\ \vdots\\ b_n
\end{array}}\right]$](Pro_matriz_files/s1img180.gif) uma matriz n x 1. Prove que
uma matriz n x 1. Prove que
AB = 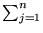 bjAj, onde
Aj é a j-ésima coluna de A.
11. Se A e B são duas matrizes tais que AB =
bjAj, onde
Aj é a j-ésima coluna de A.
11. Se A e B são duas matrizes tais que AB = 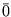 , então A =
, então A = 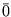 ou B =
ou B = 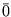 ? Justifique.
12. Dizemos que uma matriz A, n x n é
simétrica se At = A.
? Justifique.
12. Dizemos que uma matriz A, n x n é
simétrica se At = A.
- (a)
- Mostre que se A é simétrica, então
aij = aji,
para i, j = 1,...n;
- (b)
- Mostre que se A e B são simétricas, então A +
B também é simétrica e AB é simétrica se, e somente se,
AB = BA;
13. Determine todas as matrizes A, 2 x 2, tais que AB =
BA para toda matriz B, 2 x 2.
Parte da página construída por Reginaldo de Jesus Santos
Atualizada por Milton Procópio de Borba
![]() e
e![]() escalares. São válidas as seguintes propriedades para as
operações matriciais:
escalares. São válidas as seguintes propriedades para as
operações matriciais: