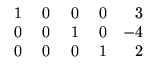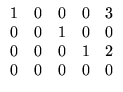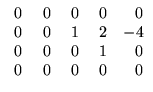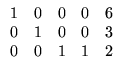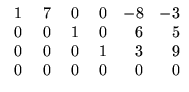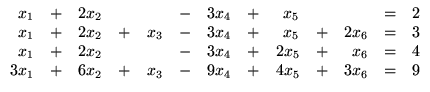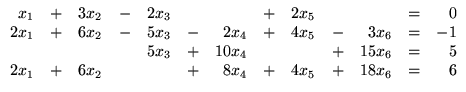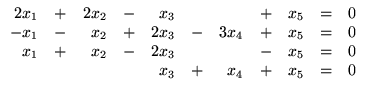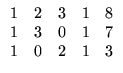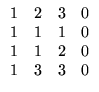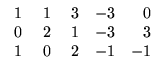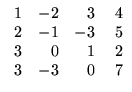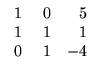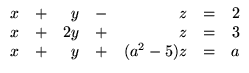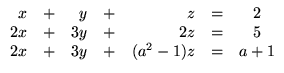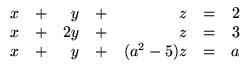Sistemas Lineares Homogêneos
Um sistema linear da forma
é chamado sistema
homogêneo. Este sistema pode ser escrito como A X = 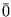 . Todo sistema homogêneo admite pelo menos a
solução X =
. Todo sistema homogêneo admite pelo menos a
solução X = 
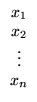
![$ \left.\vphantom{\begin{array}{c}
x_1\\ x_2\\
\vdots\\
x_n\end{array}}\right]$](Sis_homog_files/s2img149.gif) =
= 
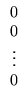
![$ \left.\vphantom{\begin{array}{c}
0\\ 0\\
\vdots\\
0\end{array}}\right]$](Sis_homog_files/s2img152.gif) chamada de solução
trivial.
chamada de solução
trivial.
Portanto, todo sistema homogêneo tem solução.
Observação. Para resolver um sistema
linear homogêneo A X = 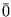 , basta escalonarmos a matriz A do
sistema, já que sob a ação de uma operação elementar a coluna de zeros não é
alterada. Mas, é preciso ficar atento quando se escreve o sistema linear
associado à matriz resultante das operações elementares, para se levar em
consideração esta coluna de zeros que não vimos escrevendo.
, basta escalonarmos a matriz A do
sistema, já que sob a ação de uma operação elementar a coluna de zeros não é
alterada. Mas, é preciso ficar atento quando se escreve o sistema linear
associado à matriz resultante das operações elementares, para se levar em
consideração esta coluna de zeros que não vimos escrevendo.
Teorema. Se
A = (aij)m
x n, é tal que m < n, então o sistema homogêneo AX = 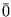 tem solução diferente da solução trivial, ou seja, todo sistema
homogêneo com menos equações do que incógnitas tem infinitas soluções.
tem solução diferente da solução trivial, ou seja, todo sistema
homogêneo com menos equações do que incógnitas tem infinitas soluções.
Demonstração. Como o sistema tem menos
equações do que incógnitas (m < n), o número de linhas não
nulas r da forma escalonada reduzida da matriz aumentada do sistema
também é tal que r < n. Assim, temos pelo menos n -
r incógnitas livres, que podem assumir qualquer valor. Logo, o sistema
admite solução não trivial. 
Exemplo. O conjunto solução de um
sistema linear homogêneo satisfaz duas propriedades importantes:
- 1.
- Se X e Y são soluções do sistema homogêneo AX =
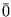 , então AX =
, então AX = 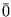 e AY =
e AY = 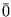 e portanto X + Y também é solução pois, A(X +
Y) = AX + AY =
e portanto X + Y também é solução pois, A(X +
Y) = AX + AY = 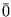 +
+ 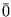 =
= 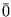 ;
;
- 2.
- Se X é solução do sistema homogêneo
AX =
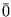 , então
, então 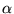 X também o é, pois A(
X também o é, pois A(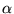 X) =
X) = 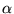 AX =
AX = 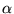
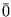 =
= 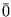 .
.
Portanto, se X e Y são soluções de um sistema
homogêneo, então X + Y e 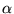 X também o são. Estas propriedades não são válidas para sistemas
lineares em geral. Por exemplo, considere o sistema linear
A X = B, onde A = [1] e B = [1]. A
solução deste sistema é X = [1]. Mas, X
+ X = 2 X = 2, não é solução do sistema.
X também o são. Estas propriedades não são válidas para sistemas
lineares em geral. Por exemplo, considere o sistema linear
A X = B, onde A = [1] e B = [1]. A
solução deste sistema é X = [1]. Mas, X
+ X = 2 X = 2, não é solução do sistema.
Exercícios
Numéricos
- 1.
- Quais das seguintes matrizes estão na forma escalonada reduzida:
A = 
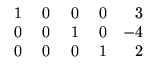
![$ \left.\vphantom{\begin{array}{rrrrr}
\;1&\;0&\;0&\;0&3\\
0&0&1&0&-4\\ 0&0&0&1&2
\end{array}}\right]$](Sis_homog_files/s2img155.gif) ,
B =
,
B = 

![$ \left.\vphantom{\begin{array}{rrrrr}
\;0&\;1&\;0&0&-4\\
0&0&1&0&5\\ 0&0&0&-1&2
\end{array}}\right]$](Sis_homog_files/s2img161.gif) ,
,
C = 
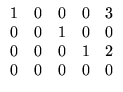
![$ \left.\vphantom{\begin{array}{rrrrr} 1&0&0&0&3\\ 0&0&1&0&0\\ 0&0&0&1&2\\
0&0&0&0&0
\end{array}}\right]$](Sis_homog_files/s2img158.gif) ,
D =
,
D = 
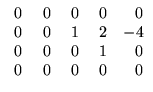
![$ \left.\vphantom{\begin{array}{rrrrr}
\;0&\;0&\;0&\;0&0\\
0&0&1&2&-4\\ 0&0&0&1&0\\ 0&0&0&0&0
\end{array}}\right]$](Sis_homog_files/s2img164.gif) .
.
- 2.
- Em cada item suponha que a matriz aumentada de um sistema foi transformada
usando operações elementares a matriz escalonada reduzida dada. Resolva o
sistema.
- (a)
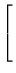

![$ \left.\vphantom{\begin{array}{rrrrr}
\;1&\;0&\;0&-7&8\\
0&1&0&3&2\\ 0&0&1&1&-5
\end{array}}\right]$](Sis_homog_files/s2img167.gif) ;
(b)
;
(b) 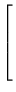

![$ \left.\vphantom{\begin{array}{rrrrrr}
\;1&-6&\;0&\;0&\;3&-2\\
0&0&1&0&4&7\\ 0&0&0&1&5&8\\ 0&0&0&0&0&0
\end{array}}\right]$](Sis_homog_files/s2img170.gif) ;
;
- (c)
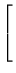
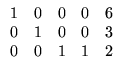
![$ \left.\vphantom{\begin{array}{rrrrr} 1&0&0&0&6\\ 0&1&0&0&3\\ 0&0&1&1&2
\end{array}}\right]$](Sis_homog_files/s2img173.gif) ;
(d)
;
(d) 
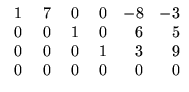
![$ \left.\vphantom{\begin{array}{rrrrrr}
\;1&\;7&\;0&\;0&-8&-3\\
0&0&1&0&6&5\\ 0&0&0&1&3&9\\ 0&0&0&0&0&0
\end{array}}\right]$](Sis_homog_files/s2img176.gif) .
.
3.
Resolva, usando o método de Gauss-Jordan, os seguintes sistemas:
- (a)
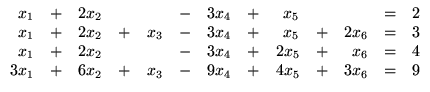
 ;
;
- (b)
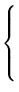
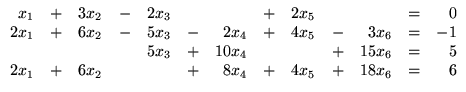
 ;
;
- (c)
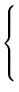
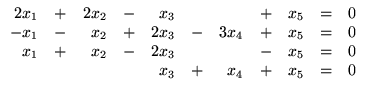
 .
.
4.
Resolva os sistemas lineares cujas matrizes aumentadas são:
- (a)
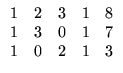
![$ \left.\vphantom{\begin{array}{rrrrr} 1&2&3&1&8\\ 1&3&0&1&7\\ 1&0&2&1&3
\end{array}}\right]$](Sis_homog_files/s2img188.gif) ;
(b)
;
(b) 
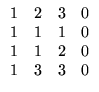
![$ \left.\vphantom{\begin{array}{rrrr} 1&2&3&0\\ 1&1&1&0\\ 1&1&2&0\\ 1&3&3&0
\end{array}}\right]$](Sis_homog_files/s2img191.gif) ;
;
- (c)
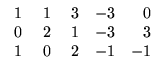
![$ \left.\vphantom{\begin{array}{rrrrr}
\;1&\;1&\;3&-3&0\\
0&2&1&-3&3\\ 1&0&2&-1&-1
\end{array}}\right]$](Sis_homog_files/s2img194.gif) ;
(d)
;
(d) 
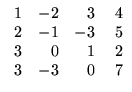
![$ \left.\vphantom{\begin{array}{rrrrr}
\;1&-2&3&\;4\\
2&-1&-3&5\\ 3&0&1&2\\ 3&-3&0&7
\end{array}}\right]$](Sis_homog_files/s2img197.gif) .
.
5.
Seja
- (a)
- Encontre a solução geral do sistema
(- 4I3 -
A)X =
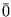 ;
;
- (b)
- Encontre a solução geral do sistema
(2I3 - A)X
=
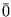 ;
;
6.
Para cada sistema linear dado, encontre todos os valores de a para
os quais o sistema não tem solução, tem solução única e tem infinitas
soluções:
- (a)
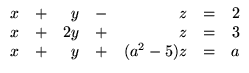
 ;
;
- (b)
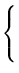
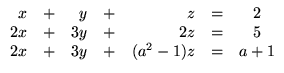
 ;
;
- (c)
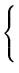
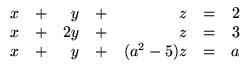
 ;
;
Exercícios
Teóricos
7. Mostre que se X é solução de um sistema linear
A X = B, então X também é solução de
C X = D, onde [C | D] é
obtida de [A | B] aplicando-se uma operação
elementar sobre suas linhas.
8. Mostre que toda operação elementar possui inversa, do mesmo tipo, ou seja,
para cada operação elementar existe uma outra operação elementar do mesmo tipo
que desfaz o que a operação anterior fez.
9. Prove:
(a) Toda matriz é equivalente por linhas a ela mesma;
(b) Se A é equivalente por linhas a B, então B é
equivalente por linhas a A;
(c) Se A é equivalente por linhas a B e B é equivalente
por linhas a C, então A é equivalente por linhas a C.
10. Seja A uma matriz quadrada, n
x n, na forma escalonada reduzida. Mostre que se A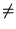 In, então A tem uma
linha nula.
In, então A tem uma
linha nula.
11. Sejam X1 e X2 soluções do sistema
homogêneo A X = 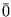 .
.
(a) Mostre que 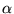 X1 +
X1 + 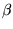 X2 é solução, para
quaisquer escalares
X2 é solução, para
quaisquer escalares 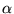 e
e 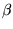 ;
;
(b) Mostre que o item anterior não é verdadeiro para sistemas lineares em
geral.
12. Chamamos de matriz elementar uma matriz
obtida aplicando-se uma operação elementar na matriz identidade. Seja E
uma matriz elementar de ordem n. Mostre que se aplicamos em uma matriz
A, de ordem n, a mesma operação elementar que originou E
obteremos a matriz E A.
(Sugestão: faça as contas para
matrizes de ordem 2 e depois generalize para as de ordem n)
Parte da página construída por Reginaldo de Jesus Santos
Atualizada por Milton Procópio de Borba

![]() , basta escalonarmos a matriz A do
sistema, já que sob a ação de uma operação elementar a coluna de zeros não é
alterada. Mas, é preciso ficar atento quando se escreve o sistema linear
associado à matriz resultante das operações elementares, para se levar em
consideração esta coluna de zeros que não vimos escrevendo.
, basta escalonarmos a matriz A do
sistema, já que sob a ação de uma operação elementar a coluna de zeros não é
alterada. Mas, é preciso ficar atento quando se escreve o sistema linear
associado à matriz resultante das operações elementares, para se levar em
consideração esta coluna de zeros que não vimos escrevendo.
![]() tem solução diferente da solução trivial, ou seja, todo sistema
homogêneo com menos equações do que incógnitas tem infinitas soluções.
tem solução diferente da solução trivial, ou seja, todo sistema
homogêneo com menos equações do que incógnitas tem infinitas soluções.
![]()