Sistemas de Equações Lineares
Existem problemas em várias áreas da Ciência que recaem na solução de
sistemas lineares.
Definição.
- 1.
- Uma equação linear em n variáveis x1,
x2,..., xn é uma equação da forma
a1x1 +
a2x2 +...+
anxn = b ,
onde a1,
a2,..., an e b são constantes
reais;
- 2.
- Um sistema de equações lineares ou simplesmente sistema
linear é um conjunto de equações lineares, ou seja, é um conjunto de
equações da forma
onde aij e bk são constantes reais,
para i, k = 1,..., m e j = 1,..., n.
Usando as operações matriciais que definimos na seção anterior, o sistema
linear acima pode ser escrito como uma equação matricial
AX = B ,
onde
Uma solução de um sistema linear é uma matriz S = 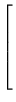
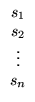
![$ \left.\vphantom{\begin{array}{c} s_1\\ s_2\\
\vdots\\
s_n\end{array}}\right]$](Selas_files/s2img19.gif) tal que as equações do sistema são satisfeitas quando substituimos x1 =
s1, x2 = s2,...,
xn = sn. O conjunto de todas as soluções do
sistema é chamado conjunto solução ou solução geral do sistema.
tal que as equações do sistema são satisfeitas quando substituimos x1 =
s1, x2 = s2,...,
xn = sn. O conjunto de todas as soluções do
sistema é chamado conjunto solução ou solução geral do sistema.
Exemplo. O sistema linear de duas
equações e duas incógnitas
pode ser escrito como
A solução (geral) do sistema acima é x = - 1/3 e y = 2/3 ou
Uma forma de resolver um sistema linear é substituir o sistema inicial
por outro que tenha o mesmo conjunto solução do primeiro, mas que seja mais
fácil de resolver. O outro sistema é obtido depois de aplicar sucessivamente uma
série de operações sobre as equações. As operações que são usadas são:
- Troca de posição entre duas equações do sistema;
- Multiplicação de uma equação por um escalar diferente de zero;
- Somar a uma equação um múltiplo de outra equação.
Estas operações são chamadas de
operações elementares. Quando aplicamos operações elementares sobre as
equações de um sistema linear somente os coeficientes do sistema são alterados,
assim podemos aplicar as operações sobre a matriz de coeficientes do sistema,
que chamamos de matriz aumentada, ou seja, a matriz
Definição. Uma operação elementar
sobre as linhas de uma matriz é uma das seguintes operações:
- 1.
- Troca da posição de duas linhas;
- 2.
- Multiplicação de uma linha da matriz por um escalar (número) diferente de
zero;
- 3.
- Somar a uma linha da matriz um múltiplo de outra linha.
O método que vamos usar para resolver sistemas lineares consiste na
aplicação de operações elementares às linhas da matriz aumentada do sistema até
que ela esteja numa forma em que o sistema associado a esta matriz seja de fácil
resolução. Vamos procurar ``deixar'' a matriz numa forma em que todas as linhas
nulas estejam abaixo das linhas não nulas, todas as linhas não nulas possuam
como primeiro elemento não nulo o número 1 (será chamado
de pivô). Além disso, se uma coluna contém um pivô, então todos os seus
outros elementos terão que ser iguais a zero. Vamos ver no exemplo seguinte como
conseguimos isso.
Exemplo.
Considere o seguinte sistema
A sua matriz aumentada é
1a. eliminação: Vamos procurar para pivô da 1a. linha um elemento
não nulo da primeira coluna (podemos usar a troca de linhas para ``trazê-lo''
para a primeira linha). Como temos que fazer o pivô igual a um, escolhemos para
pivô o elemento de posição 2 1. Precisamos ``colocá-lo'' na primeira linha,
para isto, trocamos a 2a. linha com a 1a.
Agora, precisamos ``zerar'' os outros elementos da 1a. coluna, que é a
coluna do pivô, para isto, adicionamos à 2a. linha, -2 vezes a 1a. linha e
adicionamos à 3a. linha, -1 vezes a 1a. linha.
2a. eliminação: Olhamos para a sub-matriz obtida eliminando-se a
1a. linha. Escolhemos para pivô um elemento diferente de zero na 1a. coluna não
nula desta sub-matriz. Pela mesma razão que na 1a. eliminação vamos escolher o
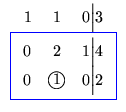
elemento de posição 3 2. Precisamos ``colocá-lo'' na 2a. linha, para isto,
trocamos a 3a. linha com a 2a.
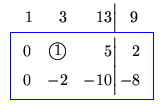
Agora, precisamos zerar os outros elementos da 2a. coluna, que é a coluna
do pivô, para isto, somamos à 3a. linha, -2 vezes a 2a. e somamos à 1a. linha,
-1 vezes a 2a.
Portanto o sistema dado é equivalente ao sistema
que possui solução geral dada por
A última matriz que obtivemos está na forma que
chamamos de escalonada reduzida.
Definição. Uma matriz A = (aij)m
x n está na forma escalonada reduzida quando satisfaz as
seguintes condições:
- 1.
- Todas as linhas nulas (formadas inteiramente por zeros) ocorrem abaixo das
linhas não nulas;
- 2.
- O primeiro elemento não nulo de cada linha não nula é igual a 1 (chamado
de pivô);
- 3.
- O pivô da linha i + 1 ocorre à direita do pivô da linha i,
para i = 1,..., m - 1.
- 4.
- Se uma coluna contém um pivô, então todos os seus outros elementos são
iguais a zero;
Se uma matriz satisfaz as propriedades (a), (b) e
(c), mas não necessariamente (d), dizemos que ela é uma matriz
escalonada.
Exemplo. As matrizes
são escalonadas reduzidas.
Definição.
Uma matriz A =
(aij)m x n é equivalente por linhas
a uma matriz B =
(bij)m x n, se B pode ser obtida de
A aplicando-se uma seqüência de operações elementares sobre as suas
linhas.
Exemplo. Observando o Exemplo
acima, vemos que a matriz aumentada do sistema
é equivalente por linhas à matriz
que é escalonada reduzida. Além disso, se fizermos qualquer operação
elementar sobre suas linhas a matriz resultante não será mais escalonada
reduzida, ou seja, a forma reduzida escolonada é única. Em geral, qualquer
matriz é equivalente por linhas a uma única matriz escalonada reduzida e a
demonstração, que omitiremos, pode ser feita da mesma forma que fizemos com o
caso particular do exemplo anterior.
Este método de resolução de sistemas é conhecido como o método de Gauss-Jordan.
Teorema. Toda matriz A = (aij)m
x n é equivalente por linhas a uma única matriz escalonada
reduzida R =
(rij)m x n.
Exemplo. Considere o seguinte sistema
A sua matriz aumentada é
1a. eliminação:
Como temos que fazer o pivô igual a um,
escolhemos para pivô o elemento de posição 4 1. Precisamos ``colocá-lo'' na
primeira linha, para isto, trocamos a 4a. linha com a 1a.
Agora, precisamos ``zerar'' os outros elementos da 1a. coluna, que é a
coluna do pivô, para isto, adicionamos à 2a. linha, -5 vezes a 1a. e adicionamos
à 3a. linha, -4 vezes a 1a.
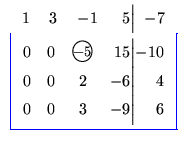
2a. eliminação:
Olhamos para a sub-matriz obtida eliminando-se
a 1a. linha. Escolhemos para pivô um elemento diferente de zero na 1a. coluna
não nula desta sub-matriz. Escolhemos o elemento 2 3. Como temos que fazer
o pivô igual a 1, multiplicamos a 2a. linha por -1/5.
Agora, precisamos zerar os outros elementos da 2a. coluna, que é a coluna
do pivô, para isto, adicionamos à 1a. linha a 2a. , adicionamos à 3a. linha, -2
vezes a 2a. e à 4a. linha, -3 vezes a 2a.
Esta matriz é escalonada reduzida. Portanto o sistema dado é equivalente
ao sistema seguinte
A matriz deste sistema possui duas colunas sem pivô. Portanto, temos duas
variáveis livres, isto é, podem assumir valores arbitrários. Vamos
considerar as variáveis y e w (que não estão associadas a nenhum
pivô) variáveis livres.
Sejam w = 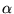 e y =
e y = 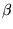 . As variáveis associadas aos pivôs terão os seus valores dependentes
das variáveis livres. Assim, a solução geral do sistema é
. As variáveis associadas aos pivôs terão os seus valores dependentes
das variáveis livres. Assim, a solução geral do sistema é
Exemplo.
Considere o seguinte sistema
A sua matriz aumentada é
1a. eliminação:
Como o pivô da 1a. linha é igual a 1 e os
outros elementos da 1a. coluna são iguais a zero, não há nada o que fazer na 1a.
eliminação.
2a. eliminação:
Olhamos para submatriz obtida eliminando-se a
1a. linha. Escolhemos para pivô um elemento não nulo da 1a. coluna não nula da
submatriz. Escolhemos o elemento de posição 2 2. Como ele é igual a 1,
precisamos, agora, ``zerar'' os outros elementos da coluna do pivô. Para isto
somamos à 1a. linha, -3 vezes a 2a. e somamos à 3a. linha, 2 vezes a 2a.
Portanto o sistema dado é equivalente ao sistema
que não possui solução.
Teorema. Se as matrizes aumentadas de
dois sistemas lineares AX = B e CX = D, [A
| B] e [C | D] são equivalentes por
linhas então os sistemas possuem as mesmas soluções.
Demonstração. A demonstração deste
teorema segue de duas observações que faremos a seguir:
- (1)
- Se X é solução de um sistema, então X também é solução do
sistema obtido aplicando-se uma operação elementar sobre suas equações (por
que?).
- (2)
- Se o sistema CX = D, pode ser obtido de AX = B
aplicando-se operações elementares às suas equações (ou equivalentemente às
linhas da matriz aumentada), então o sistema AX = B também pode
ser obtido de CX = D aplicando-se operações elementares, pois
cada operação elementar possui uma operação elementar inversa (que desfaz!)
(verifique!).
Pela definição de equivalente por linhas
e pela observação (2), AX = B e CX = D podem ser obtidos um do outro aplicando-se operações elementares sobre
as suas linhas. E pela observação (1), os dois possuem as mesmas soluções. 
Observação. Para se encontrar a solução
de um sistema linear não é necessário transformar a matriz aumentada do sistema
na sua forma escalonada reduzida, mas se a matriz está nesta forma, o sistema
associado é o mais simples possível.
Exemplo. Considere um sistema linear
A X = B, que possua duas soluções distintas X0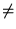 X1. Vamos mostrar que esse sistema possui infinitas
soluções. Seja
X1. Vamos mostrar que esse sistema possui infinitas
soluções. Seja
X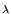
= (1 -
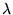
)
X0 +
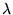 X1
X1, para
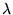
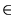
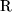
.
Vamos mostrar que X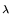 é solução do sistema A X = B, para
qualquer
é solução do sistema A X = B, para
qualquer 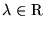 . Para isto vamos mostrar que
A X
. Para isto vamos mostrar que
A X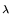 = B. Aplicando as propriedades (9), (10) das operações
matriciais (ver Teorema ) obtemos
= B. Aplicando as propriedades (9), (10) das operações
matriciais (ver Teorema ) obtemos
A X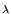
=
A[(1 -
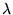
)
X0 +
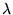 X1
X1] =
A(1 -
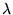
)
X0 +
A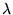 X1
X1 = (1 -
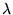
)
A X0 +
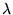 A X1
A X1
Como X0 e X1 são soluções de
A X = B, então A X0 =
B e A X1 = B, portanto
A X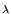
= (1 -
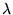
)
B +
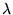 B
B = [(1 -
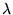
) +
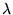
]
B =
B,
pela propriedade (6) do mesmo Teorema.
Assim o sistema A X = B tem infinitas soluções, pois
para qualquer valor de 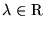 , X
, X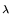 é solução.
é solução.
Observe que para 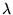 = 0, X
= 0, X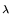 = X0, para
= X0, para 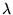 = 1, X
= 1, X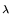 = X1, para
= X1, para 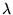 = 1/2,
X
= 1/2,
X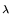 =
= 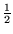 X0 +
X0 + 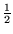 X1,
X1,
para 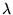 = 3, X
= 3, X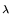 = - 2X0 + 3X1 e para
= - 2X0 + 3X1 e para 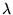 = - 2, X
= - 2, X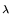 = 3X0 - 2X1.
= 3X0 - 2X1.
Suponha que escalonamos a matriz aumentada de um sistema linear de
m equações e n incógnitas. Observe que o pivô de uma linha
i está sempre numa coluna j, com j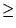 i. E por isso, o número de linhas não nulas é
sempre menor ou igual a n + 1. Dependendo da forma da última linha não
nula podemos classificar o sistema quanto ao número de soluções:
i. E por isso, o número de linhas não nulas é
sempre menor ou igual a n + 1. Dependendo da forma da última linha não
nula podemos classificar o sistema quanto ao número de soluções:
- Se a última linha não nula é da forma [ 0...0 |
b'p ], com b'p
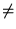 0, então o sistema associado não tem
solução
0, então o sistema associado não tem
solução
( ver Exemplo ).
- Se a última linha não nula é a linha n e é da forma [ 0...0 1 | b'n ]
, então o sistema correspondente tem solução única, pois isto força a
que todos os pivôs estejam na diagonal e toda variável esteja associada a um
pivô
( ver exemplo ).
- Se a última linha não nula é a linha p, com p < n
e o pivô da linha p está na coluna k, com k
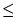 n. Então o sistema tem infinitas
soluções. Pois,
n. Então o sistema tem infinitas
soluções. Pois,
- se k < n, então a última linha é da forma [ 0...0 1 a'p(k
+ 1)...a'pn| b'p ], o
que implica que as variáveis
xk + 1,...,
xn não estão associadas a nenhum pivô. Por isso, estas
variáveis podem ser consideradas variáveis livres
( ver exemplo );
- se p < k
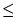 n, então pelo menos uma coluna é da
forma
[a'1j...a'(j
- 1)j 0...0 ]t, o que implica que a variável
xj não está associada a nenhum pivô. Por isso,
xj pode ser considerada uma variável livre
n, então pelo menos uma coluna é da
forma
[a'1j...a'(j
- 1)j 0...0 ]t, o que implica que a variável
xj não está associada a nenhum pivô. Por isso,
xj pode ser considerada uma variável livre
( ver exemplo ).
Vale a pena, ainda, ver: Sistemas Lineares Homogêneos
Parte da página construída por Reginaldo de Jesus Santos
Atualizada por Milton Procópio de Borba



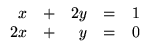
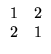
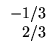
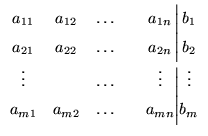
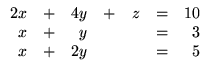
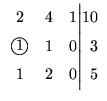
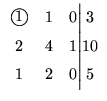
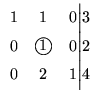
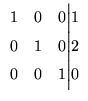
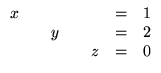
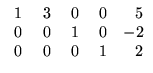
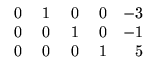
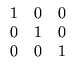
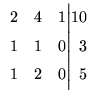
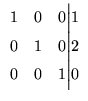
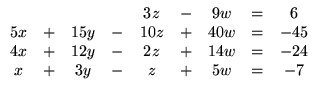
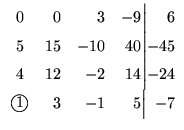
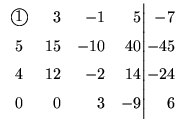
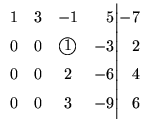
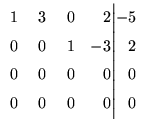
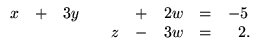
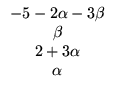
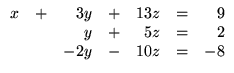
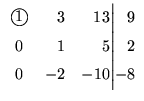
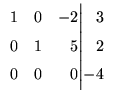
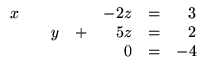
![]() X1. Vamos mostrar que esse sistema possui infinitas
soluções. Seja
X1. Vamos mostrar que esse sistema possui infinitas
soluções. Seja
![]() i. E por isso, o número de linhas não nulas é
sempre menor ou igual a n + 1. Dependendo da forma da última linha não
nula podemos classificar o sistema quanto ao número de soluções:
i. E por isso, o número de linhas não nulas é
sempre menor ou igual a n + 1. Dependendo da forma da última linha não
nula podemos classificar o sistema quanto ao número de soluções: