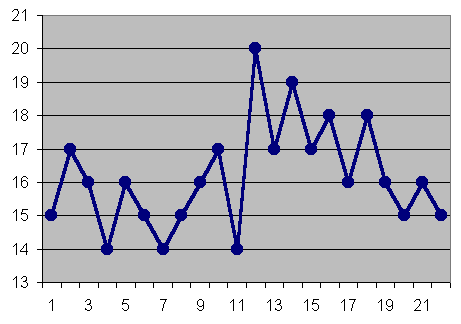
Valores assumidos por uma ação numa Bolsa de Valores
| Relações e Funções | |||
|---|---|---|---|
Ao lermos um jornal ou uma revista, diariamente nos deparamos com gráficos, tabelas e ilustrações. Estes, são instrumentos muito utilizados nos meios de comunicação. Um texto com ilustrações, é muito mais interessante, chamativo, agradável e de fácil compreensão. Não é só nos jornais ou revistas que encontramos gráficos. Os gráficos estão presentes nos exames laboratoriais, nos rótulos de produtos alimentícios, nas informações de composição química de cosméticos, nas bulas de remédios, enfim em todos os lugares. Ao interpretarmos estes gráficos, verificamos a necessidade dos conceitos de plano cartesiano e de produto cartesiano.
Ao relacionarmos espaço em função do tempo, número do sapato em função do tamanho dos pés, intensidade da fotossíntese realizada por uma planta em função da intensidade de luz a que ela é exposta ou pessoa em função da impressão digital, percebemos quão importantes são os conceitos de funções para compreendermos as relações entre os fenômenos físicos, biológicos, sociais...
Observamos então que as aplicações de plano cartesiano, produto cartesiano, relações e funções estão presentes no nosso cotidiano.

O plano cartesiano ortogonal é constituído por dois eixos perpendiculares entre si
( OX e OY ) que se cruzam na origem. O eixo horizontal é o eixo das
abscissas (eixo OX) e o eixo vertical é o eixo das ordenadas (eixo OY).
Associando a cada um dos eixos o conjunto de todos os números reais, obtém-se o
plano cartesiano ortogonal. Cada ponto P(a,b) do plano cartesiano é
formado por um par ordenado de números, indicados entre parênteses, a abscissa (a) e
a ordenada (b) respectivamente. Este par ordenado representa as coordenadas (a,b) do ponto P. O primeiro número indica o deslocamento a partir da origem para a direita (se
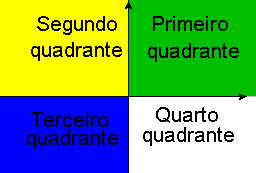
for positivo) ou para a esquerda (se for negativo). Os dois eixos dividem o plano em quatro regiões denominadas quadrantes sendo
que tais eixos são retas concorrentes na origem do sistema formando um ângulo
reto (90 graus). Os nomes dos quadrantes são indicados no sentido anti-horário,
conforme a figura (com as cores da bandeira do Brasil, em homenagem ao "penta").
Dados dois conjuntos A e B não vazios, definimos o produto cartesiano entre A
e B, denotado por AxB, como o conjunto de todos os pares ordenados da forma
(x,y) onde x pertence ao primeiro conjunto A e y pertence ao segundo conjunto B.
Observe que AxB Se A possui m elementos e B possui n elementos, então AxB
possui mxn elementos.
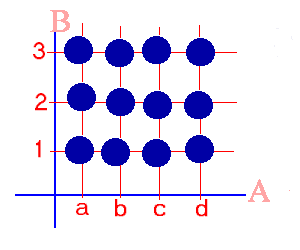
Exemplo: Dados A = {a, b, c, d} e B = {1,
2, 3}, o produto cartesiano AxB, terá 12 pares ordenados e será dado por:
Sejam A e B conjuntos não vazios. Uma relação em AxB é qualquer subconjunto R
de AxB.
A relação mostrada na figura acima é:
Como, por exemplo, (a,3) A relação R em AxB pode ainda ser dita R de A em B e ser denotada por R: A Exemplo: Se A={1,2} e B={3,4} então
AxB={(1,3),(1,4),(2,3),(2,4)} e neste caso, temos algumas relações em AxB:
Nem sempre uma relação está definida sobre todo o conjunto universo. As relações mais importantes são aquelas definidas em subconjuntos. O conjunto A é o domínio da relação R, denotado por Dom(R),
Exemplos e representações gráficas de relações em
AxB
Seja R uma relação de A em B. A relação inversa de R, denotada por
R-1, é definida de B em A por:
Exemplo: Sejam A={a,b,c}, B={d,e,f} e R uma
relação em AxB, definida por:
R-1 = {(d,a),(f,a),(d,b),(e,b),(f,b),(d,c),(f,c)}
Observação importante:
Exemplo: Seja A= {a,b,c}. Uma relação
reflexiva deve ter os segunintes elementos:
Exemplo: Seja A={a,b,c}. Uma relação
simétrica é:
Exemplo: Seja A={a,b,c}. Uma relação
transitiva é:
Exemplo: Seja A={a,b,c}. Uma relação
anti-simétrica em A é:
O Plano Cartesiano
Referência
históricaOs nomes Plano Cartesiano e Produto Cartesiano
são homenagens ao seu criador René Descartes (1596-1650), filósofo e
matemático francês. O nome de Descartes em Latim, era Cartesius, daí vem o
nome cartesiano. 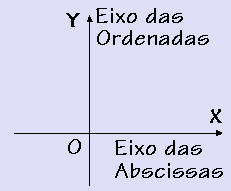
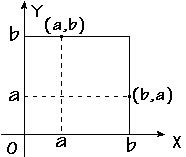
O segundo número indica o
deslocamento a partir da origem para cima (se for positivo) ou para baixo (se
for negativo).
Observe no desenho, em anexo, que: (a,b) 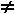 (b,a) se a
(b,a) se a  b.
b.
Produto Cartesiano
 A e y
A e y B }
B }  BxA,
se A é não vazio ou B é não vazio. Se A=Ø ou B=Ø, por definição: AxØ=Ø=ØxB.
BxA,
se A é não vazio ou B é não vazio. Se A=Ø ou B=Ø, por definição: AxØ=Ø=ØxB.
Relações no Plano Cartesiano
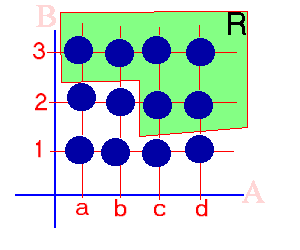
 R, isto significa que a está relacionado a 3 por R.
R, isto significa que a está relacionado a 3 por R.
Podemos, ainda dizer que R relaciona a a 3 e escrever aR3.
![]() B.
B.
Domínio, Contradomínio e Imagem de uma Relação
Para evitar problemas, pode-se definir uma relação R: A B, da seguinte forma:
B, da seguinte forma:
O conjunto B é o contradomínio da relação R, denotado por CoDom(R) e
A imagem é o subconjunto de B, efetivamente usado pela relação R. A :
existe y
A :
existe y  B tal que
(x,y)
B tal que
(x,y) R}
R}  B : existe x
B : existe x  A tal que (x,y)
A tal que (x,y) R}
R} 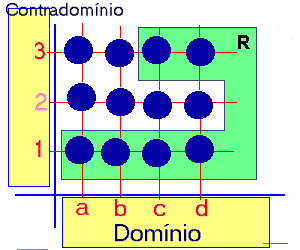
R1 = {(a,1),(a,2),(a,3),(b,1),(b,2),(b,3),(c,1),
(d,1),(d,2),(d,3)}
Dom(R1) = { a , b , c , d }
CoDom(R1) = { 1 , 2 , 3 }
Im(R1) = { 1 , 2 , 3 }
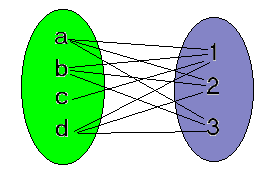
R2 = {(a,1),(a,2),(c,3),(d,1)}
Dom(R2) = { a , b , c , d }
CoDom(R2) = { 1 , 2 , 3 }
Im(R2) = { 1 , 2 , 3 }
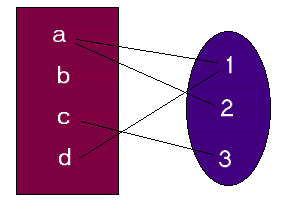
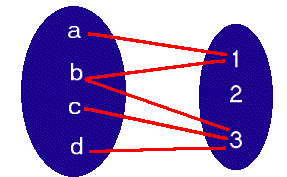
R3 = {(a,1),(b,1),(b,3),(c,3),(d,3)}
Dom(R3) = { a , b , c , d }
CoDom(R3) = { 1 , 2 , 3 }
Im(R3) = { 1 , 3 }
Relações Inversas
 BxA : (x,y)
BxA : (x,y) R}
R}
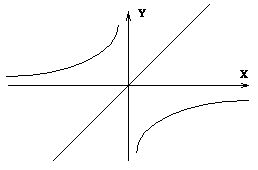
O gráfico da
relação inversa R-1 é simétrico ao gráfico da relação R, em relação à
reta y=x (identidade).
Propriedades de Relações
Ver, ainda: Outros exemplos
Uma relação R em AxA é reflexiva se
todo elemento de A se relaciona consigo mesmo, ou seja, para todo x em A:
(x,x) R, ou ainda, para
todo x em A: xRx.
R, ou ainda, para
todo x em A: xRx.
Uma relação R em AxA é simétrica se
x estiver relacionado com y, então necessariamente y deverá estar relacionado
com x, ou seja:
Quaisquer que sejam x A e y
A e y A, tem-se que (x,y)
A, tem-se que (x,y) R implica que (y,x)
R implica que (y,x) R.
R.
Uma relação R em AxA é transitiva,
se x estiver relacionado com y e y estiver relacionado com z, então x deverá
estar relacionado com z, ou seja:
Quaisquer que sejam x A, y
A, y A, z
A, z A, se (x,y)
A, se (x,y) R e (y,z)
R e (y,z) R então (x,z)
R então (x,z) R.
R.
Sejam x A e y
A e y A. Uma relação R é anti-simétrica se
(x,y)
A. Uma relação R é anti-simétrica se
(x,y) R e (y,x)
R e (y,x) R implicar que x=y.
Alternativamente, uma relação é anti-simétrica se x e y são elementos
distintos do conjunto A então x não tem relação com y ou
(exclusivo) y não tem relação com x, o que significa que o par de
elementos distintos (x,y) do conjunto A poderá estar na relação desde que o
par (y,x) não esteja.
R implicar que x=y.
Alternativamente, uma relação é anti-simétrica se x e y são elementos
distintos do conjunto A então x não tem relação com y ou
(exclusivo) y não tem relação com x, o que significa que o par de
elementos distintos (x,y) do conjunto A poderá estar na relação desde que o
par (y,x) não esteja.
|
histórica |
Leonhard Euler (1707-1783), médico, teólogo, astrônomo e matemático suíço, desenvolveu trabalhos em quase todos os ramos da Matemática Pura e Aplicada, com destaque para a Análise - estudo dos processos infinitos - desenvolvendo a idéia de função. Foi o responsável também pela adoção do símbolo f(x) para representar uma função de x. Hoje, função é uma das idéias essenciais em Matemática. |
Uma função f de A em B é uma relação em AxB, que associa a cada variável x em A, um único y em B.
Uma das notações para uma função de A em B, é:
Quatro aspectos chamam a atenção na definição apresentada:
Estas características nos informam que uma função definida num intervalo I real pode ser vista
geometricamente como uma linha no plano, contida em IxB, que só pode ser
"cortada" uma única vez por uma reta vertical, qualquer que seja esta reta passando por I.
A relação R = {(x,y) Dom(R) = I = [-a,a]
Exemplos importantes de funções reais
Sejam a e b números reais não nulos. Uma função afim é uma função
f: R Exemplos: As funções f: R O gráfico de uma função afim é uma reta oblíqua que não passa pela origem (0,0).
Exemplos: As funções f: R O gráfico de uma função linear é uma reta que passa pela origem (0,0).
Como nem toda relação é uma função, às vezes, alguns elementos poderão não
ter correspondentes associados para todos os números reais e para evitar
problemas como estes, costuma-se definir o Domínio de uma função f, denotado por
Dom(f), como o conjunto onde esta relação f tem significado.
Consideremos a função real que calcula a raiz quadrada de um número real.
Deve estar claro que a raiz quadrada de -1 não é um número real, assim como não
são reais as raízes quadradas de quaisquer números negativos, dessa forma o
domínio desta função só poderá ser o intervalo [0,+infinito), onde a raiz
quadrada tem sentido sobre os reais.
Como nem todos os elementos do contradomínio de uma função f estão
relacionados, define-se a Imagem de f, denotada por Im(f), como o
conjunto de todos os elementos do contradomínio que estão relacionados com
elementos do domínio de f, isto é:
Note que se uma relação R é uma função de A em B, então A é o domínio e B é o
contradomínio da função e se x é um elemento do domínio de uma função f, então a
imagem de x é denotada por f(x).
Exemplos
e seu gráfico é dado por:
e seu gráfico é dado por:
Uma função f: A
Exemplos
Uma função f: A Exemplos
Uma função f: A Exemplo: A função f: R
Uma função real f é par se, qualquer que seja x Exemplo: A função real definida por y =
f(x) = x2 é par, pois: f(-x) = (x)2 = x2 = f(x). Outra importante função par é aquela
definida por Uma função real f é ímpar se, qualquer que seja x Exemplo: As funções reais definidas por No gráfico em anexo pode-se ver a simetria no gráfico da função f.
Uma função f é crescente, se quaisquer que sejam x1 e x2 no Domínio de f, com x1<x2, tivermos
f(x1)<f(x2). Exemplo: Seja a função f: R
Uma função f é decrescente, se para quaisquer x1 <
x2 em Dom(f), tivermos f(x1)>f(x2). Exemplo: Seja a função f: R
Seja f: A
Exemplo: Sejam as funções reais definidas
por f(u) = 4u+2 e g(x) = 7x–4.
Como a variável u não é importante no contexto de uma função, ela poderia ser
substituída por x e teríamos:
De um modo geral, fog é diferente de gof.
Exemplo: Consideremos as funções reais
definida por f(x) = x2+1 e g(x )= 2x–4. Então:
Dada uma função bijetora f: A Observação: Uma característica
importantíssima aqui é que se g é a inversa de f, f é a inversa de g e valem as
relações:
onde IA e IB são, respectivamente, as funções
identidades nos conjuntos A e B. Esta característica algébrica nos permite
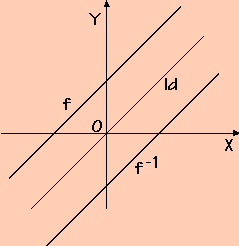
afirmar que os gráfico de f e de sua inversa de f são simétricos em relação à
função identidade (y = x).
Exemplo:
Sejam A = {1, 2, 3, 4, 5} e B = {2, 4, 6, 8, 10}.
Seja f: R Podemos confirmar o resultado (exercício) mostrando que
Com o gráfico podemos observar a simetria em relação à reta identidade.
A partir de funções f e g, podemos realizar algumas operações, entre as
quais:
Uma função polinomial real tem a forma
e ela tem as seguintes características:
Exemplo: A área de um quadrado pode ser
representada pela função real f(x) = x2 onde x é a medida do lado do
quadrado, enquanto que o volume de um cubo pode ser dado pela função real
f(x) = x3 onde x é a medida da aresta do cubo.
As funções polinomiais são extremamente úteis na vida. Uma aplicação simples
pode ser realizada quando se pretende obter o volume de uma caixa (sem tampa) na
forma de paralelepípedo que se pode construir com uma chapa metálica quadrada
com 20 cm de lado, com a retirada de pequenos quadrados de lado igual a x nos
quatro cantos da chapa.
Com esta função, é possível obter valores ótimos para a construção desta
caixa.
 Relações que não são funções
Relações que não são funções
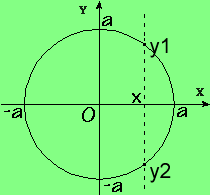
 R2: x2 + y2 = a2}
não é uma função, pois se tomarmos a reta vertical (linha tracejada no desenho)
, teremos duas correspondentes ordenadas (y1 e y2) para a mesma abscisa x = 3a/5.
R2: x2 + y2 = a2}
não é uma função, pois se tomarmos a reta vertical (linha tracejada no desenho)
, teremos duas correspondentes ordenadas (y1 e y2) para a mesma abscisa x = 3a/5.
Im(R) = [-a,a].
Seja A={a,b,c,d} e B={1,2,3}. A relação R4={(a,1), (a,3), (b,2),
(c,3), (d,3)} não é uma função em AxB, pois associado ao mesmo
valor a existem dois valores distintos, que são 1 e 3.
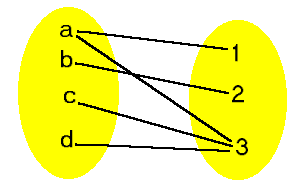
Seja A={a,b,c,d} e B={1,2,3}
A relação R5={(a,1),
(a,3), (b,2), (c,3)} não é uma função em AxB, pois nem todos os elementos
do primeiro conjunto A estão associados a elementos do segundo conjunto
B.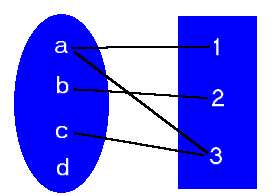
( f: R![]() R , onde R = conjunto dos números reais )
R , onde R = conjunto dos números reais )
![]() R que para cada x
em R, associa y = f(x)= ax+b.
R que para cada x
em R, associa y = f(x)= ax+b.
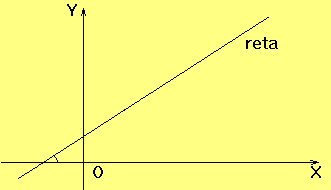
![]() R definidas por:
R definidas por:
Seja a um número real.
Uma função linear é uma função f: R![]() R que para cada x em R, associa y = f(x) = ax.
R que para cada x em R, associa y = f(x) = ax.
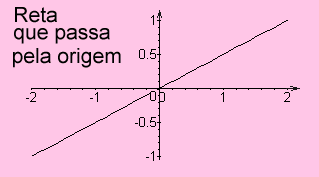
![]() R definidas por:
R definidas por:
Domínio, Contradomínio e Imagem de uma função
 B :
existe x
B :
existe x A tal que y = f(x)
}
A tal que y = f(x)
}
 R, definida por y = f(x) = x2, tem as características:
R, definida por y = f(x) = x2, tem as características:
 R, definida por
y = f(x) = x2, tem as características:
R, definida por
y = f(x) = x2, tem as características:
 R, definida por y = f(x) = |x|, conhecida por função modular ,tem as características:
R, definida por y = f(x) = |x|, conhecida por função modular ,tem as características:
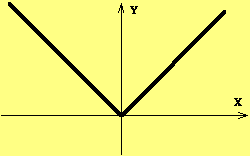
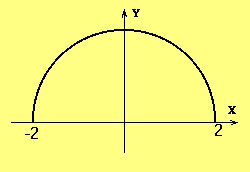
![]() representa uma
semi-circunferência e tem as características:
representa uma
semi-circunferência e tem as características:
Funções Injetoras, Sobrejetoras e Bijetoras
 B é injetora se
dois elementos distintos quaisquer de A sempre duas têm imagens distintas em B,
isto é:
B é injetora se
dois elementos distintos quaisquer de A sempre duas têm imagens distintas em B,
isto é:
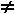 x2 implica que f(x1)
x2 implica que f(x1) 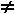 f(x2)
f(x2)
 R definida por y = f(x) = 3x+2 é injetora, pois sempre que tomamos valores diferentes para x,
encontramos valores diferentes para f(x).
R definida por y = f(x) = 3x+2 é injetora, pois sempre que tomamos valores diferentes para x,
encontramos valores diferentes para f(x).
 R definida por y= f(x) = x2+5 não é injetora, pois para x = 1 temos f(1) = 6 e para x = -1
temos f(-1) = 6.
R definida por y= f(x) = x2+5 não é injetora, pois para x = 1 temos f(1) = 6 e para x = -1
temos f(-1) = 6.  B é sobrejetora
se todo elemento de B é a imagem de pelo menos um elemento de A. Isto equivale a
afirmar que a imagem da função deve ser exatamente igual ao contradomínio da
função = B, ou seja, para todo y em B existe x em A tal que y = f(x).
B é sobrejetora
se todo elemento de B é a imagem de pelo menos um elemento de A. Isto equivale a
afirmar que a imagem da função deve ser exatamente igual ao contradomínio da
função = B, ou seja, para todo y em B existe x em A tal que y = f(x).
 R definida por y= f(x) = 3x+2 é sobrejetora, pois todo elemento de R é imagem de um elemento de R
pela função.
R definida por y= f(x) = 3x+2 é sobrejetora, pois todo elemento de R é imagem de um elemento de R
pela função.
 R+ definida
por y = f(x) = x2 é sobrejetora, pois todo elemento de R+ é
imagem de pelo menos um elemento de R pela função.
R+ definida
por y = f(x) = x2 é sobrejetora, pois todo elemento de R+ é
imagem de pelo menos um elemento de R pela função.
 R definida por y = f(x) = 2x não é sobrejetora, pois o número –1 é elemento do contradomínio
R e não é imagem de qualquer elemento do domínio.
R definida por y = f(x) = 2x não é sobrejetora, pois o número –1 é elemento do contradomínio
R e não é imagem de qualquer elemento do domínio.  B é bijetora se
ela é ao mesmo tempo injetora e sobrejetora.
B é bijetora se
ela é ao mesmo tempo injetora e sobrejetora.
 R dada por y = f(x) = 2x é bijetora, pois é injetora e bijetora.
R dada por y = f(x) = 2x é bijetora, pois é injetora e bijetora.
Funções Pares e Ímpares
![]() Dom(f), tem-se que f(x) = f(-x).
Dom(f), tem-se que f(x) = f(-x).
Uma função par possui o gráfico simétrico em relação ao eixo vertical OY.
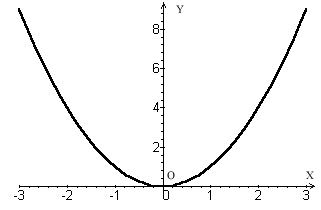
Observe a simetria do gráfico de f.
g(x) = cos(x), pois g(-x) = cos(-x) = cos(x) = g(x).
![]() Dom(f), tem-se que f(-x) = -f(x).
Dom(f), tem-se que f(-x) = -f(x).
Uma
função ímpar possui o gráfico simétrico em relação à origem do sistema
cartesiano.
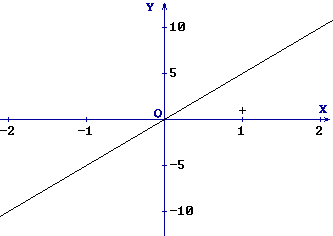
y = f(x) = 5x e y = g(x) = sen(x) são ímpares, pois
f(-x) = 5(-x) = -5x = -f(x) e
g(-x) = sen(-x) = -sen(x) = -g(x).
Funções crescentes e decrescentes
Isto é, conforme o valor de x aumenta, o
valor da imagem de x pela função também aumenta.
 R definida por y = f(x) = 8x+2.
R definida por y = f(x) = 8x+2.
Tomando em particular os valores: x1 = 1 e x2 = 2, teremos que
f(x1) = 10 e f(x2) = 18.
Como o gráfico de f é uma reta,
x1<x2 e f(x1)<f(x2) então a
função é crescente.
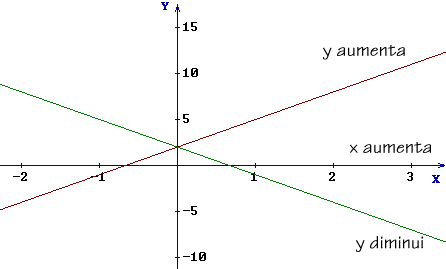
Isto é, conforme o valores de x aumentam, os valores da imagem de x pela função f diminuem.
 R definida por y = f(x) = -8x+2.
R definida por y = f(x) = -8x+2.
Tomando em particular: x1 = 1 e x2 = 2, teremos que f(x1) = -6 e
f(x2) = -14.
Como o gráfico de f é uma reta, x1<x2 e f(x1)>f(x2), a função é decrescente.
Funções Compostas
 B, g:B
B, g:B C duas funções. Chama-se composta de f com g,
denotada por gof, a função definida por gof(x) = g(f(x)). A expressão gof pode ser lida como
"g bola f".
C duas funções. Chama-se composta de f com g,
denotada por gof, a função definida por gof(x) = g(f(x)). A expressão gof pode ser lida como
"g bola f".
Para que a composição ocorra o Im(f) deve ser subconjunto de Dom(g).
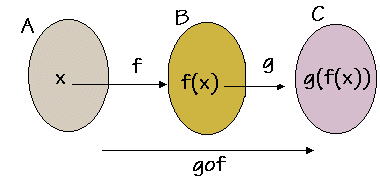
A composições fog e gof são possíveis e neste caso
serão definidas por:
(gof)(u) =
g(f(u)) = g(4u + 2) = 7(4u + 2) – 4 = 28u + 10
(gof)(x) = g(f(x)) = g(x2+1) =
2(x2+1)–4 = 2x2 -2
Funções Inversas
 B,
denomina-se função inversa de f à função
B,
denomina-se função inversa de f à função
g:B A tal que se f(a) = b, então g(b) = a, quaisquer
que sejam a
A tal que se f(a) = b, então g(b) = a, quaisquer
que sejam a![]() A e b
A e b![]() B.
B.
Denotaremos a função inversa de f por f-1.
Consideremos a função f: A B
definida por f(x) = 2x e g: B
B
definida por f(x) = 2x e g: B A definida por
g(x) = x/2. Obervemos nos gráficos abaixo as situações das setas indicativas das
ações das funções.
A definida por
g(x) = x/2. Obervemos nos gráficos abaixo as situações das setas indicativas das
ações das funções.
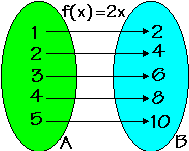
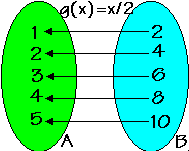
Processo algébrico para obter a inversa de uma
função
 R,
dada poy y = f(x) = x+3.
R,
dada poy y = f(x) = x+3.
Na equação y = x+3, trocando x por y e y por x, teremos x = y+3 e
isolando y obteremos y = x–3.
Assim, g(x) = x–3 é a função inversa de f(x) = x+3.
fog = gof = Identidade.
Operações com Funções
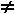 0
0
Funções Polinomiais
Dom(f) = R
CoDom(f) = R
Im(f)=???
Aplicação da função polinomial
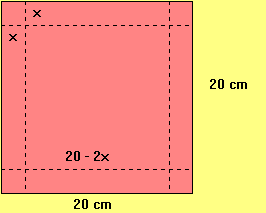 V(x)=(20-2x)2.x
V(x)=(20-2x)2.x
Atualizada por Milton Procópio de Borba