Como
aplicação, vamos ao problema de Kepler. Na origem do sistema de coordenadas está
o Sol, de massa 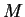 . O vetor
. O vetor 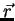 vai do Sol à Terra, de massa
vai do Sol à Terra, de massa 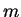 . A força, segundo Newton, é
. A força, segundo Newton, é
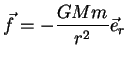 |
(47) |
Como o vetor 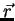 é
é
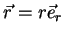 |
(48) |
temos
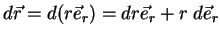 |
(49) |
Usando (30),
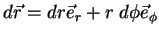 |
(50) |
e, "dividindo" por 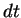 ,
,
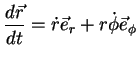 |
(51) |
onde usamos a notação de Newton: o ponto sobre o símbolo significa sua
derivada no tempo.
A derivada segunda de 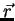 não oferece novas dificuldades.
não oferece novas dificuldades.
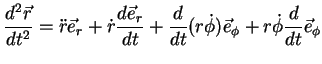 |
(52) |
As derivadas dos vetores de base podem facilmente ser calculadas usando
(30)
e (31).
Obtemos:
Levando este resultado a (52),
obtemos
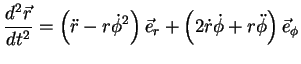 |
(55) |
A lei de Newton assume então a forma:
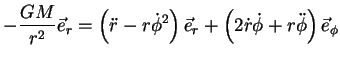 |
(56) |
Igualando os coeficientes dos vetores, temos as equações procuradas:
O prosseguimento em direção à obtenção das soluções consiste, em primeiro
lugar, em notar que, multiplicando a segunda, termo a termo, por 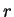 , podemos reescrevê-la assim:
, podemos reescrevê-la assim:
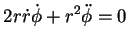 |
(59) |
que é a mesma coisa que
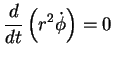 |
(60) |
ou ainda
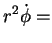 constante constante |
(61) |
Não é dificil identificar esta constante (considerando, por exemplo, o
caso particular de órbita circular): trata-se do momento angular por unidade de
massa. Logo, introduzindo a notação
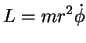 |
(62) |
para o momento angular, podemos escrever
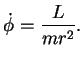 |
(63) |
Inserindo este resultado em (57) e
remexendo um pouco, obtemos a equação
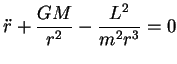 |
(64) |
Resolvendo-se esta equação diferencial para 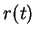 e usando-a em
e usando-a em
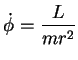 |
(65) |
podemos determinar 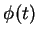 . Isto determina completamente o movimento
(Para um tratamento completo deste problema, veja Sommerfeld, Mechanics, §6, pg.38.)
Vamos fazer uma análise qualitativa do
movimento, usando a equação (64).
Esta equação não contém o ângulo
. Isto determina completamente o movimento
(Para um tratamento completo deste problema, veja Sommerfeld, Mechanics, §6, pg.38.)
Vamos fazer uma análise qualitativa do
movimento, usando a equação (64).
Esta equação não contém o ângulo 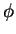 . Pode ser pensada como a equação de movimento como visto por um
observador que gira junto com a Terra, e só percebe o movimento radial. Como não
é um sistema inercial, devemos estar prontos para achar forças de inércia.
. Pode ser pensada como a equação de movimento como visto por um
observador que gira junto com a Terra, e só percebe o movimento radial. Como não
é um sistema inercial, devemos estar prontos para achar forças de inércia.
De fato, multiplicando (64) por
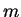 , temos
, temos
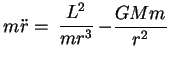 |
(66) |
ou seja, a massa vezes a aceleração (neste sistema a única aceleração é a
radial) é igual à força de Newton mais uma força que é zero se o momento angular
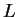 for zero. Esta força é chamada de "força
centrífuga", e é uma força de inércia.
for zero. Esta força é chamada de "força
centrífuga", e é uma força de inércia.
Multiplicando termo a termo por 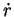 , obtemos
, obtemos
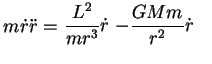 |
(67) |
que pode ser escrita assim:
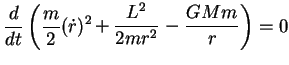 |
(68) |
ou seja,
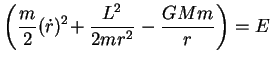 |
(69) |
onde 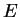 é uma constante. Podemos interpretar esta equação assim: a energia
é uma constante. Podemos interpretar esta equação assim: a energia
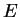 é constituída da energia cinética
é constituída da energia cinética 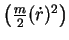 mais a energia potencial, que vem em duas partes: uma atrativa,
mais a energia potencial, que vem em duas partes: uma atrativa, 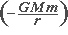 e uma repulsiva,
e uma repulsiva, 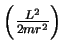 . Denotando por
. Denotando por 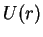 a soma das duas energias potenciais, temos o seguinte gráfico:
a soma das duas energias potenciais, temos o seguinte gráfico:
O movimento só é permitido nas regiões onde 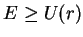 , do contrário teríamos energias cinéticas
negativas, o que é impossível. Se o planeta tem energia
, do contrário teríamos energias cinéticas
negativas, o que é impossível. Se o planeta tem energia 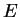 como na figura, seu movimento radial se dá entre os dois
pontos em que a linha tracejada corta a curva de
como na figura, seu movimento radial se dá entre os dois
pontos em que a linha tracejada corta a curva de 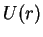 , denotados na figura por
, denotados na figura por 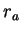 e
e 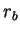 . Há então um valor máximo e um mínimo de
. Há então um valor máximo e um mínimo de 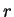 , correspondendo ao movimento elíptico com o perihélio e o afélio
sendo, respectivamente,
, correspondendo ao movimento elíptico com o perihélio e o afélio
sendo, respectivamente, 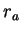 e
e 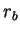 . Notem que, para a reta da energia que tangencia a curva de de
. Notem que, para a reta da energia que tangencia a curva de de 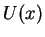 (no seu mínimo), temos um único valor possível
para
(no seu mínimo), temos um único valor possível
para 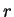 : a órbita é circular. Vemos assim que, para um
determinado momento angular fixo, a órbita de menor energia é a órbita circular.
: a órbita é circular. Vemos assim que, para um
determinado momento angular fixo, a órbita de menor energia é a órbita circular.
Henrique Fleming (junho de 2004)
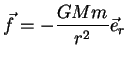
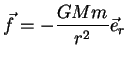
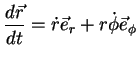
![]() não oferece novas dificuldades.
não oferece novas dificuldades.
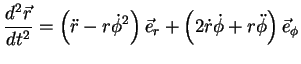
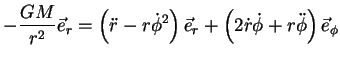
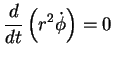
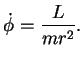
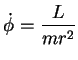
![]() , temos
, temos
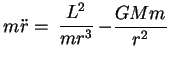
![]() , obtemos
, obtemos
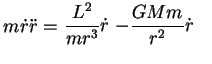
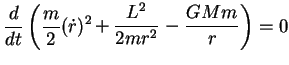
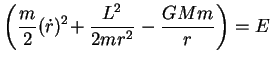
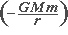 e uma repulsiva,
e uma repulsiva, 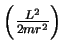 . Denotando por
. Denotando por {$r_{a}$}
\uput[0](4.1,1.3){$r_{b}$}
\end{pspicture}](Kepler_arq/img254.png)
![]() , do contrário teríamos energias cinéticas
negativas, o que é impossível. Se o planeta tem energia
, do contrário teríamos energias cinéticas
negativas, o que é impossível. Se o planeta tem energia ![]() como na figura, seu movimento radial se dá entre os dois
pontos em que a linha tracejada corta a curva de
como na figura, seu movimento radial se dá entre os dois
pontos em que a linha tracejada corta a curva de ![]() , denotados na figura por
, denotados na figura por ![]() e
e ![]() . Há então um valor máximo e um mínimo de
. Há então um valor máximo e um mínimo de ![]() , correspondendo ao movimento elíptico com o perihélio e o afélio
sendo, respectivamente,
, correspondendo ao movimento elíptico com o perihélio e o afélio
sendo, respectivamente, ![]() e
e ![]() . Notem que, para a reta da energia que tangencia a curva de de
. Notem que, para a reta da energia que tangencia a curva de de ![]() (no seu mínimo), temos um único valor possível
para
(no seu mínimo), temos um único valor possível
para ![]() : a órbita é circular. Vemos assim que, para um
determinado momento angular fixo, a órbita de menor energia é a órbita circular.
: a órbita é circular. Vemos assim que, para um
determinado momento angular fixo, a órbita de menor energia é a órbita circular.