As
coordenadas cartesianas são as mais usadas, mas não são as únicas. Para determinar
o vetor 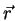 , que
vai da origem ao ponto
, que
vai da origem ao ponto 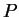 ,
podemos dar as três componentes cartesianas de
,
podemos dar as três componentes cartesianas de 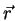 , que
vêm a ser as três coordenadas cartesianas de
, que
vêm a ser as três coordenadas cartesianas de 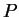 , mas
também podemos dar o tamanho do vetor, sua direção e seu sentido.
, mas
também podemos dar o tamanho do vetor, sua direção e seu sentido.
Coordenadas Polares
Como um exemplo não-trivial do uso de coordenadas curvilíneas, vamos tratar
do Problema de Kepler (Terra em redor do Sol). Como se sabe, a trajetória de uma
planeta está contida num plano que também contém o Sol. Assim, podemos, sem
perda de generalidade, considerar o problema como sendo bidimensional o que nos
permite utilizar coordenadas polares no plano.
A conexão entre as coordenadas polares e as cartesianas é dada pelas fórmulas
e pelas inversas
Seja 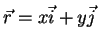 um vetor de posição. Como mostra a figura, suas
componentes ao longo dos eixos
um vetor de posição. Como mostra a figura, suas
componentes ao longo dos eixos 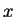 e
e
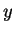 são as coordenadas do ponto localizado na sua
extremidade. Seja
são as coordenadas do ponto localizado na sua
extremidade. Seja 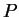 este
ponto, e
este
ponto, e 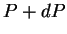 um ponto muito próximo, de coordenadas (x+dx , y+dy).
Se
um ponto muito próximo, de coordenadas (x+dx , y+dy).
Se 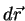 denota o vetor de
denota o vetor de  a
a
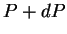 , temos
, temos
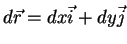 |
(5) |
Se denotarmos por 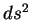 o
quadrado da distância entre
o
quadrado da distância entre 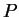 e
e
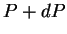 , temos
, temos
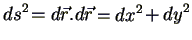 |
(6) |
Para construir uma base apropriada para as coordenadas polares, vamos
calcular 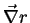 e
e 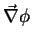 :
:
ou seja,
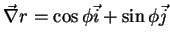 |
(8) |
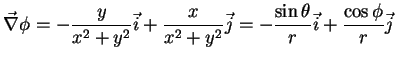 |
(9) |
Para ter uma base ortonormal, escolhemos
isto é,
Diferentemente de 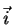 e
e
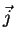 , os vetores da base adaptada às coordenadas
polares (Cartan falava na "base natural" das coordenadas polares) não são
constantes. Fala-se, então, numa "base móvel", ou "referencial móvel"
(moving frame). Já que são funções, calculemos suas diferenciais (serão úteis):
, os vetores da base adaptada às coordenadas
polares (Cartan falava na "base natural" das coordenadas polares) não são
constantes. Fala-se, então, numa "base móvel", ou "referencial móvel"
(moving frame). Já que são funções, calculemos suas diferenciais (serão úteis):
Estes dois vetores podem ser expandidos na base formada por 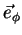 e
e 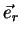 .
Usando a notação de Cartan, pomos
.
Usando a notação de Cartan, pomos
Uma aplicação interessante de referencial móvel pode ser visto ao equacionar as superfícies
Mola helicoidal e Faixa de Möbius, usando os referenciais {T,
N, B}
(Triedro de Frénet, formado pelos vetores Tangente, Normal e Binormal de uma curva,
que neste caso é o eixo destas superfícies).
Antes de prosseguir no cálculo, vamos fazer uma digressão sobre coordenadas
curvilíneas num contexto um pouco mais geral.
Coordenadas Quaisquer
Sejam 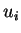 (
( 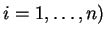 ,
coordenadas curvilíneas num espaço que admite um sistema de coordenadas
cartesianas. A expressão das
,
coordenadas curvilíneas num espaço que admite um sistema de coordenadas
cartesianas. A expressão das 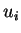 em
termos das coordenadas cartesianas é conhecida. Construímos, calculando os
gradientes das funções
em
termos das coordenadas cartesianas é conhecida. Construímos, calculando os
gradientes das funções 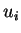 e
normalizando, os vetores
e
normalizando, os vetores 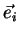 , (
, ( 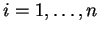 ), tais que
), tais que
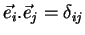 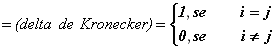 |
(18) |
Diferenciando ambos os membros, temos
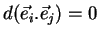 |
(19) |
ou
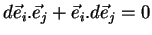 |
(20) |
Ora,
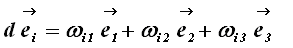 |
(21) |
logo,
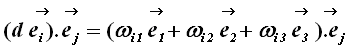 |
(22) |
e, como 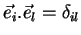 ,
temos
,
temos
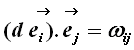 |
(23) |
e , usando
(20), obtemos que
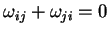 |
(24) |
Daqui se conclui que
Voltando às Coordenadas Polares, vemos que as expressões em (16)
podem ser simplificadas, pois
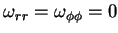 e
e 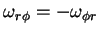 .
.
Para calcular 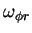 , lembremo-nos de que, numa base ortonormal,
, lembremo-nos de que, numa base ortonormal,
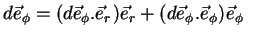 |
(27) |
Comparando com (17),
chegamos a
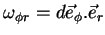 |
(28) |
O produro escalar acima é facil de calcular:
Conclui-se então que
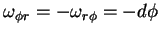 |
(29) |
e que, portanto,
Podemos, agora, voltar ao Problema de Kepler
Coordenadas Esféricas
Neste sistema, usamos o tamanho do vetor, sua direção e seu sentido, ou seja, o módulo
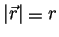 e dois ângulos que podem ser os ângulos
e dois ângulos que podem ser os ângulos 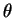 e
e 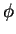 da
figura. As coordenadas esféricas do ponto
da
figura. As coordenadas esféricas do ponto 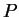 são,
então,
são,
então, 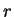 ,
, 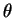 e
e
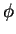 .
.
A relação entre as coordenadas cartesianas e esféricas é dada por
sendo as inversas dadas por
As coordenadas cartesianas referem-se à base fixa formada pelos vetores
unitários 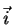 ,
,
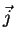 e
e 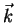 . De
fato, o vetor de posição
. De
fato, o vetor de posição 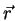 , que
termina no ponto
, que
termina no ponto 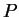 , tem
projeções ao longo dos eixos dessa base que são exatamente as coordenadas de
, tem
projeções ao longo dos eixos dessa base que são exatamente as coordenadas de
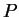 . Note-se que
. Note-se que
Qual será a base que, para as coordenadas esféricas, desempenha o papel
da base 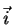 ,
,
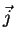 ,
, 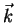 ? A
pista está dada pelas equações acima: devemos procurar os vetores que são os
gradientes das funções
? A
pista está dada pelas equações acima: devemos procurar os vetores que são os
gradientes das funções 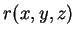 ,
, 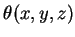 ,
, 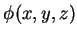 .
.
Temos:
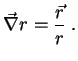 |
(38) |
Logo, temos o primeiro vetor da base,
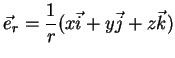 |
(39) |
Analogamente, podemos calcular 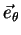 :
:
Finalmente, calculamos 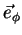 :
:
Verifica-se sem qualquer dificuldade que os vetores 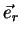 ,
, 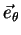 e
e 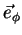 são
ortogonais, e que
são
ortogonais, e que 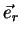 é unitário. Contudo,
é unitário. Contudo,
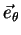 é
tal que
é
tal que
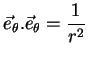 |
(40) |
e 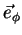 é
tal que
é
tal que
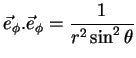 |
(41) |
Em princípio não há qualquer problema em usar uma base de vetores não
unitários. Porém, uma base ortonormal tem os seus confortos, e então preferimos usar os vetores
Em termos desta base, seja 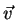 um
vetor que começa no ponto
um
vetor que começa no ponto 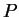 .
Então podemos escrever
.
Então podemos escrever
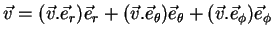 |
(45) |
ou
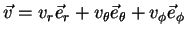 |
(46) |
Usando as relações sobre Coordenadas Gerais, podemos encontras as diferenciais deste sistema
(ver em Maple).
Henrique Fleming (junho de 2004)
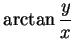
{$x$}
\uput[0](3.5,4.4){$y$}
\end{pspicture}](Coo_files/img167.png)
![]() um vetor de posição. Como mostra a figura, suas
componentes ao longo dos eixos
um vetor de posição. Como mostra a figura, suas
componentes ao longo dos eixos ![]() e
e
![]() são as coordenadas do ponto localizado na sua
extremidade. Seja
são as coordenadas do ponto localizado na sua
extremidade. Seja ![]() este
ponto, e
este
ponto, e ![]() um ponto muito próximo, de coordenadas (x+dx , y+dy).
Se
um ponto muito próximo, de coordenadas (x+dx , y+dy).
Se ![]() denota o vetor de
denota o vetor de ![]() a
a
![]() , temos
, temos
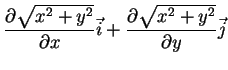
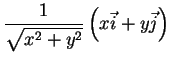
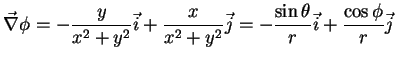
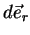
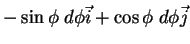
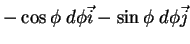
![]() (
( ![]() ,
coordenadas curvilíneas num espaço que admite um sistema de coordenadas
cartesianas. A expressão das
,
coordenadas curvilíneas num espaço que admite um sistema de coordenadas
cartesianas. A expressão das ![]() em
termos das coordenadas cartesianas é conhecida. Construímos, calculando os
gradientes das funções
em
termos das coordenadas cartesianas é conhecida. Construímos, calculando os
gradientes das funções ![]() e
normalizando, os vetores
e
normalizando, os vetores ![]() , (
, ( ![]() ), tais que
), tais que
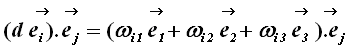
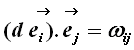
![]() e
e ![]() .
.
![]() , lembremo-nos de que, numa base ortonormal,
, lembremo-nos de que, numa base ortonormal,
(5.5,2)
\psline[linewidth...
...}
\uput[0](1.5,5.4){$z$}
\uput[0](3,4){$P$}
\uput[0](2.5,3){$r$}
\end{pspicture}](Coo_files/img119.png)
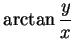
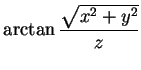
![]() ,
,
![]() e
e ![]() . De
fato, o vetor de posição
. De
fato, o vetor de posição ![]() , que
termina no ponto
, que
termina no ponto ![]() , tem
projeções ao longo dos eixos dessa base que são exatamente as coordenadas de
, tem
projeções ao longo dos eixos dessa base que são exatamente as coordenadas de
![]() . Note-se que
. Note-se que 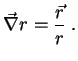
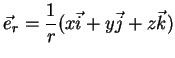
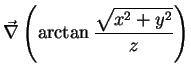
![$\displaystyle \frac{1}{r^2}\frac{1}{\sqrt{x^2+y^2}}\left[xz\vec{i}
+yz\vec{j}-(x^2+y^2)\vec{k}\right]$](Coo_files/img145.png)
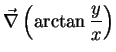
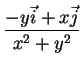
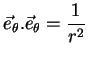
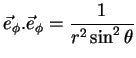
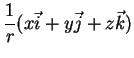
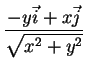
![$\displaystyle \frac{1}{r}\frac{1}{\sqrt{x^2+y^2}}
\left[xz\vec{i}+yz\vec{j}-(x^2+y^2)\vec{k}\right]$](Coo_files/img161.png)