Considere que temos três potes com capacidades de 8, 5 e 3 litros, respectivamente, os quais não possuem qualquer marcação. O maior deles esta completamente cheio enquanto que os outros dois estão vazios. Estamos interessados em dividir o vinho em duas porções iguais de 4 litros, tarefa esta que pode ser realizada por transvasos sucessivos de um pote no outro. Qual o menor número de transvasos necessários para completar a divisão?
Sejam c1 = 8, c2 = 5 e c3 = 3 respectivamente as capaciades dos três potes p1, p2 e p3. Então, um possível modelo para este problema é definir o grafo G(V,A) como:
V = { (q1, q2, q3) | q1, q2 e q3 representam as quantidades de vinho dos três potes, sendo que:
0 =< q1 <= c1,
0 =< q2 <= c2,
0 =< q3 <= c3,
q1 + q2 + q3 = 8}
A = { (e1,e2) | o estado e2 é alcançado partindo-se do estado e1 por meio de um único transvaso de um pote para outro, cuja; o transvaso é completado quando o pote de origem é esvaziado ou quando o pote de destino é enchido}
Sejam px e py respectivamente os pote de origem e de destino do transvaso. Segundo o descrito a definição das arestas acima, um transvaso é possível se o pote de origem não estiver vazio (qx > 0) e o pote de destino não estiver cheio (qy < cy). A quantidade a ser transvasada é dada pelo mínimo entre o que tem no pote de origem (qx) e o que ainda cabe no pote de destino (cy-qy). Como resultado de um transvaso, a quantidade do pote px é descrescida em t unidades, enquanto que a quantidade do pote py é acrescida de t unidades.
| pré-condição | ação | pós-condição |
| qx > 0 e (qy < cy) e (x ¹ y) | transvaso de t =
mínimoEntre(qx,cy-qy) litros de px para py |
q'x = qx - t q'y = qy + t |
Considerando esta regra e escrevendo um algoritmo de busca em profundidade, podemos obter todos os estados alcançáveis partindo-se do estado inicial (8,0,0) até chegar ao nodo de destino (4,4,0). O algoritmo abaixo exemplifica esta busca:
grafo := Digrafo new. capacidades := #(8 5 3). self buscaEmProfundidade3PotesDe: #(8 0 0) para: #(4 4 0) jaVisitados: Set new. |
buscaEmProfundidade3PotesDe: origem para: destino jaVisitados: visitados
|qx qy cy t meio|
origem = destino ifTrue: [
^self
].
visitados add: origem.
1 to: 3 do: [:x|
1 to: 3 do: [:y|
cy := capacidades at: y.
qx := origem at: x.
qy := origem at: y.
(x ~= y and: [ qx > 0 and: [qy < cy]]) ifTrue: [
t := qx min: cy - qy.
meio := origem copy.
meio at: x put: qx - t;
at: y put: qy + t.
grafo conecta: origem a: meio.
(visitados includes: meio) ifFalse: [
self buscaEmProfundidade3PotesDe: meio para: destino
jaVisitados: visitados.
].
]
]
].
|
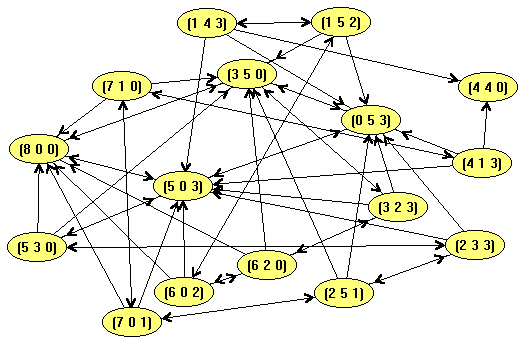
O grafo resultante desta busca é apresentado na figura que se segue.

Diferentemente do que acontece com o problema do canibais e dos missionários, neste caso não é tão fácil visualizar a solução
do problema dado que o grafo é bem mais emaranhado.
Para encontrar a melhor solução, pode-se obter o caminho de
custo mínimo que vai do nodo (8,0,0) até o (4,4,0), considerando que cada
aresta tem peso 1. Alternativamente pode-se modificar o algoritmo apresentado
acima para que ela vá guardando a melhor solução à medida que as soluções vão
sendo encontradas. O algoritmo seguinte exemplifica esta alternativa:
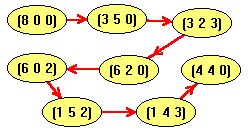
O grafo resultante da aplicação deste algoritmo, que representa a melhor
solução para o problema, é apresentado na figura que se segue:
Pode-se também fazer uma busca em largura, utilizando um algoritmo
similar ao descrito abaixo:
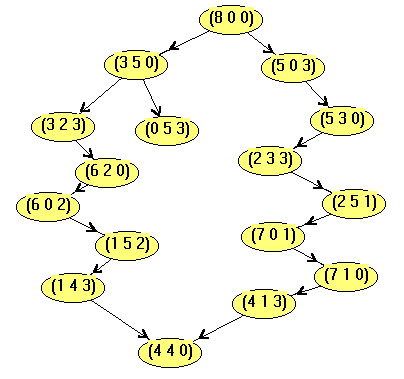
O resultado da busca em largura é apresentado na figura que se segue:
grafo := Digrafo new.
capacidades := #(8 5 3).
melhorCaminho := nil.
self buscaEmProfundidade3PotesDe: #(8 0 0) para: #(4 4 0)
caminho: OrderedCollection new.
self realcaMelhorCaminho.
buscaEmProfundidade3PotesDe: origem para: destino caminho: caminho
|qx qy cy t meio|
origem = destino ifTrue: [
(melhorCaminho isNil or:
[caminho size + 1 < melhorCaminho size])ifTrue: [
melhorCaminho := caminho copy.
melhorCaminho addLast: destino.
].
^self
].
(caminho includes: origem) ifTrue: [
^self
].
caminho addLast: origem.
1 to: 3 do: [:x|
1 to: 3 do: [:y|
cy := capacidades at: y.
qx := origem at: x.
qy := origem at: y.
(x ~= y and: [ qx > 0 and: [qy < cy]]) ifTrue: [
t := qx min: cy - qy.
meio := origem copy.
meio at: x put: qx - t;
at: y put: qy + t.
grafo conecta: origem a: meio.
self buscaEmProfundidade3PotesDe: meio para: destino
caminho: caminho.
]
]
].
caminho removeLast.
realcaMelhorCaminho
1 to: melhorCaminho size - 1 do: [:indice|
(grafo arestaDe: (melhorCaminho at: indice) para:
(melhorCaminho at: indice + 1))
cor: Vermelho;
espessura: 2.
].
grafo arestas do: [:aresta|
aresta cor = Vermelho ifFalse: [
grafo removeAresta: aresta
].
].
grafo nodos do: [:nodo|
((grafo grauDeEmissao: nodo) = 0 and:
[(grafo grauDeRecepcao: nodo) = 0])ifTrue: [
grafo removeNodo: nodo
].
].
grafo := Digrafo new.
capacidades := #(8 5 3).
self buscaEmLargura3PotesDe: #(8 0 0) para: #(4 4 0).
buscaEmLargura3PotesDe: origem para: destino
|qx qy cy t meio aVisitar proximo|
aVisitar := OrderedCollection with: origem.
[aVisitar isEmpty] whileFalse: [
proximo := aVisitar removeFirst.
1 to: 3 do: [:x|
1 to: 3 do: [:y|
cy := capacidades at: y.
qx := proximo at: x.
qy := proximo at: y.
(x ~= y and: [ qx > 0 and: [qy < cy]]) ifTrue: [
t := qx min: cy - qy.
meio := proximo copy.
meio at: x put: qx - t;
at: y put: qy + t.
meio = destino ifTrue: [
grafo conecta: proximo a: meio.
] ifFalse: [
(grafo existeNodo: meio) ifFalse: [
grafo conecta: proximo a: meio.
aVisitar addLast: meio
]
].
]
]
]
].
^false