Base ortonormal para o

Sistema de coordenadas Esféricas

por

Milton Procópio de Borba

> restart:

> with(linalg):

> with(student):

> with(LinearAlgebra): 

Warning, the protected names norm and trace have been redefined and unprotected



Warning, the assigned name GramSchmidt now has a global binding

> R:= sqrt(x*x+y*y+z*z);

> Phi:=arctan(y/x);

> Theta:=arctan(sqrt(x*x+y*y)/z);

> v:=[x,y,z];

R := sqrt(x^2+y^2+z^2)

Phi := arctan(y/x)

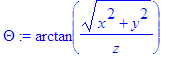
Theta := arctan((x^2+y^2)^(1/2)/z)

v := [x, y, z]

> vr:=grad(R,v);

> vf:=grad(Phi,v);

> vt:=grad(Theta,v);

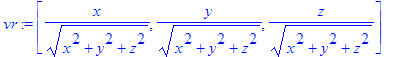
vr := vector([1/(x^2+y^2+z^2)^(1/2)*x, 1/(x^2+y^2+z...

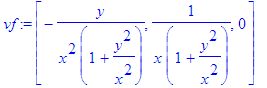
vf := vector([-y/x^2/(1+y^2/x^2), 1/(x*(1+y^2/x^2))...

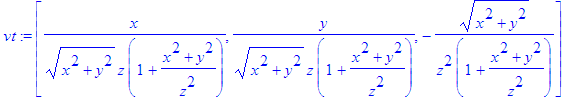
vt := vector([1/(x^2+y^2)^(1/2)/z*x/(1+(x^2+y^2)/z^...

> vr:=simplify(evalm(vr));

> vf:=simplify(evalm(vf));

> vt:=simplify(evalm(vt));

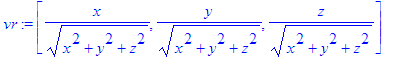
vr := vector([1/(x^2+y^2+z^2)^(1/2)*x, 1/(x^2+y^2+z...

vf := vector([-y/(x^2+y^2), x/(x^2+y^2), 0])

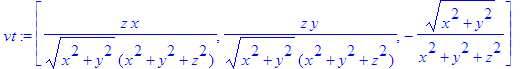
vt := vector([1/(x^2+y^2)^(1/2)*z*x/(x^2+y^2+z^2), ...

> mr:=simplify(sqrt(vr[1]^2+vr[2]^2+vr[3]^2));

> mf:=simplify(sqrt(vf[1]^2+vf[2]^2+vf[3]^2));

> mt:=simplify(sqrt(vt[1]^2+vt[2]^2+vt[3]^2));

mr := 1

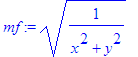
mf := sqrt(1/(x^2+y^2))

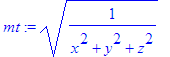
mt := sqrt(1/(x^2+y^2+z^2))

> er:=simplify(evalm(vr/mr));

> ef:=simplify(evalm(vf/mf));

> et:=simplify(evalm(vt/mt));

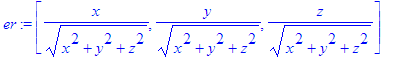
er := vector([1/(x^2+y^2+z^2)^(1/2)*x, 1/(x^2+y^2+z...

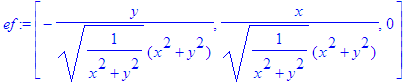
ef := vector([-1/(1/(x^2+y^2))^(1/2)*y/(x^2+y^2), 1...

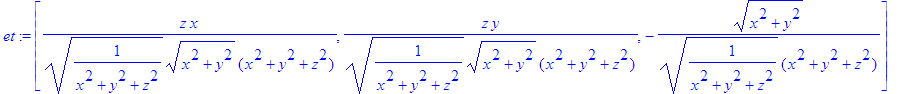
et := vector([1/(1/(x^2+y^2+z^2))^(1/2)/(x^2+y^2)^(...

Recomeçando:

> er:=convert(er, list);

> ef:=convert(ef, list);

> et:=convert(et, list);

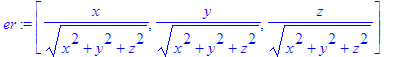
er := [1/(x^2+y^2+z^2)^(1/2)*x, 1/(x^2+y^2+z^2)^(1/...

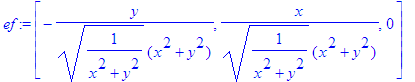
ef := [-1/(1/(x^2+y^2))^(1/2)*y/(x^2+y^2), 1/(1/(x^...

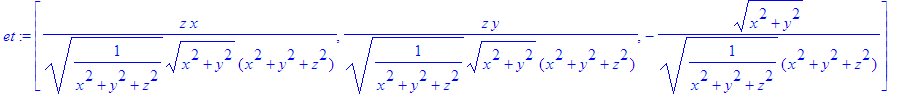
et := [1/(1/(x^2+y^2+z^2))^(1/2)/(x^2+y^2)^(1/2)*z*...

> assume(r>0);

> er:=simplify(subs(x=r*sin(theta)*cos(phi),y=r*sin(theta)*sin(phi),z=r*cos(theta), er),trig):

> ef:=simplify(subs(x=r*sin(theta)*cos(phi),y=r*sin(theta)*sin(phi),z=r*cos(theta), ef),trig):

> et:=simplify(subs(x=r*sin(theta)*cos(phi),y=r*sin(theta)*sin(phi),z=r*cos(theta), et),trig):

> assume( sin(theta)>0):ef:=normal(subs(-1+cos(theta)^2=-sin(theta)^2,ef)):

> et:=normal(subs(1-cos(theta)^2=sin(theta)^2,et)):

> alias('theta'=theta):alias('r'=r):

> e[r]=er;

> e[phi]=ef;

> e[theta]=et;

e[r] = [sin(theta)*cos(phi), sin(theta)*sin(phi), c...

e[phi] = [-sin(phi), cos(phi), 0]

e[theta] = [cos(theta)*cos(phi), cos(theta)*sin(phi...

> der:=evalm(diff(er,phi)*d[phi]+diff(er,theta)*d[theta]);

> def:=evalm(diff(ef,phi)*d[phi]+diff(ef,theta)*d[theta]);

> det:=evalm(diff(et,phi)*d[phi]+diff(et,theta)*d[theta]);

der := vector([-d[phi]*sin(theta)*sin(phi)+d[theta]...

def := vector([-d[phi]*cos(phi), -d[phi]*sin(phi), ...

det := vector([-d[phi]*cos(theta)*sin(phi)-d[theta]...

> M[1,2]:=simplify(dotprod(der,ef,'orthogonal'),trig);

> M[1,3]:=simplify(dotprod(der,et,'orthogonal'),trig);

> M[2,3]:=simplify(dotprod(def,et,'orthogonal'),trig);

M[1,2] := d[phi]*sin(theta)

M[1,3] := d[theta]

M[2,3] := -d[phi]*cos(theta)

> for i to 3 do M[i,i]:=0:

> for j to 3 do

> if i>j then M[i,j]:=-M[j,i] fi;

> od:

> od;

M[1,1] := 0

M[2,2] := 0

M[3,3] := 0

> matrix(3, 3, (i,j) -> M[i,j]);

matrix([[0, d[phi]*sin(theta), d[theta]], [-d[phi]*...

>

Base_esf.mws ( zipado )
Coordenadas Curvilíneas / Exercícios / C V E