Mola Helicoidal / Toro

por

Milton Procópio de Borba

Raio da mola = R

Raio do aço = r

Passo = p (com p = 0 , teremos o Toro)

Vontas = v

> restart: with(linalg): with(plots):

Warning, the protected names norm and trace have been redefined and unprotected

Warning, the name changecoords has been redefined

> R:=6; r:=1.5; p:=4; v:=5;

Eixo do aço

> E:=[R*cos(t),R*sin(t),p*t/(2*Pi)];

Gráfico do eixo

> spacecurve(E, t=0..2*v*Pi,numpoints=20*v, scaling=constrained);

Derivadas = vetores velocidade e aceleração

> D1:= diff(E,t);D2:=diff(D1,t);

Seus módulos: velocidade e aceleração

> nD1:=simplify(sqrt(D1[1]^2+D1[2]^2+D1[3]^2),trig);

> nD2:=simplify(sqrt(D2[1]^2+D2[2]^2+D2[3]^2),trig);

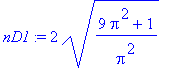
Seus unitários: velocidade e aceleração

> T:=D1/nD1; N:=D2/nD2;

O vetor binormal unitário: Produto vetorial entre T e N

> B:= simplify(crossprod(T,N),trig);

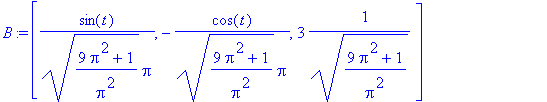
Montagem da Superfície: Eixo + r.N.cos(s) + r.B.sen(s)

> S:=evalm(E+r*N*cos(s)+r*B*sin(s));

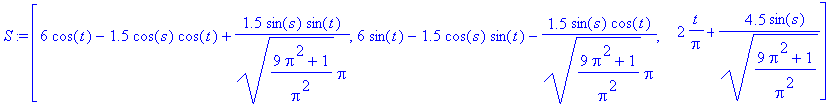
Gráfico final da mola

> plot3d(S,t=0..2*v*Pi,s=0..2*Pi,grid=[30*v,15],scaling=constrained);

Criação de 12 molas, com passos diferentes, para simular um movimento.

> for i from 1 to 6 do

> P[i] := plot3d(subs(p=(i+1)*r,op(1,S)),t=0..2*v*Pi,s=0..2*Pi,grid=[30*v,15])

> od:

> for i from 7 to 12 do

> P[i] := plot3d(subs(p=(14-i)*r,op(1,S)),t=0..2*v*Pi,s=0..2*Pi,grid=[30*v,15])

> od:

Animação das molas: marcar o gráfico e clicar na seta de "PLAY"

> display([seq(P[i],i=1..12)], insequence=true,scaling=constrained);

>
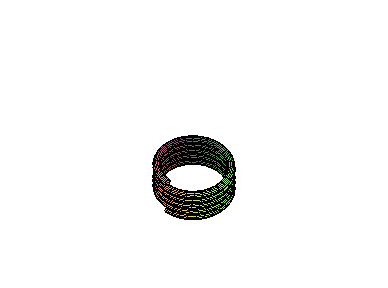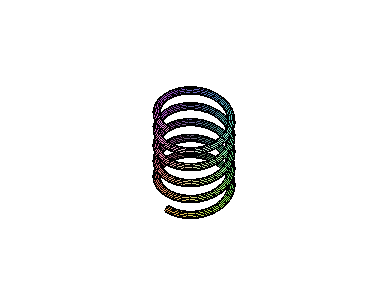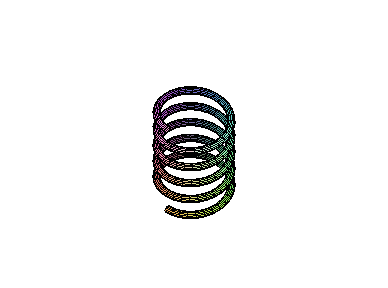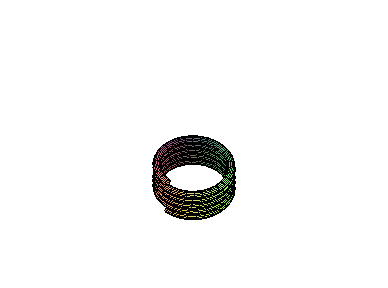