Consiste em calcular a Taxa Interna de Retorno (TIR) , necessária para "zerar" o Valor Presente dos fluxos de cada investimento. Esta é a taxa de juros obtida no investimento.
Um investimento será considerado recomendado, se tiver uma TIR não inferior à TMA.
Duração diferente
Os investimentos com durações distintas devem ser estudados adequadamente, nas duas situações:
1) PROCESSO REPETITIVO
Nestes casos (como reposição periódica de certa parte de um equipamento) devemos repeti-los até atingir uma duração igual ao mmc das durações e então teremos investimentos de mesma duração, com várias saídas e entradas.
A TIR correspondente a cada investimento será a taxa equivalente à(s) repetição(ões).
2) PROCESSO NÃO REPETITIVO
Nestes casos, pode ficar difícil decidir qual é a melhor duas situações:
ter lucro de i % a.a. durante n anos;
ter lucro de j % a.a. durante m anos,
principalmente quando j < i enquanto m > n.
Uma análise mais detalhada, é recomendada, nestes casos.
Sempre
estaremos supondo que ao escolher uma alternativa, a diferença entre a outra
não escolhida,
deverá ser aplicada à uma taxa de, no mínimo, igual à TMA, que é a melhor opção do investidor.
Este
investimento é o que chamamos de Incremental.
1) A empresa dispõe de R$ 180.000,00 e se apresentam dois equipamentos parecidos para comprar um:
-
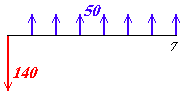
Marca A) Exigem um investimento inicial (compra e instalação) de R$ 140.000,00, e proporciona um lucro líquido anual de R$ 50.000,00, durante 7 anos.
-
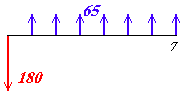
Marca B) Exigem um investimento inicial (compra e instalação) de R$ 180.000,00, e proporciona um lucro líquido anual de R$ 65.000,00, durante 7 anos.
Calcule a melhor alternativa, sob uma TMA da empresa de 30% a.a.
Solução:
TIR(A) ==>
-140.000,00
+ 50.000,00 [P/A
; i(A)
; 7] = 0 ==> [P/A] =
2,800000
==>TIR(A)
=30,03
% a.a
TIR(B) ==>
-180.000,00 + 65.000,00
[P/A ; i(B)
; 7] =
0 ==>[P/A] =
2,769231 ==>TIR(B)
= 30,51
% a.a
TIR(B - A) ==>
-40.000,00 + 15.000,00
[P/A ; i
; 7] = 0 ==>[P/A] =
2,666667 ==>TIR(B
- A)
= 32,18
% a.a
Assim, se optássemos por A, o resto (em relação ao B),
deveria ser aplicado a 32,18% a.a.
para que o investimento A fosse comparável ao B.
Como o investidor não tem esta possibilidade (sua TMA = 30%a.a.),
deve-se aplicar em B.
Este fato pode ser observado no gráfico abaixo, onde aparecem os VP, as TIR e a TMA.
 Interseção
de FISCHER
Interseção
de FISCHER
Resposta: A alternativa B é a recomendada economicamente. Obtém lucro de 30,51 % a.a
2) Idem 1), se a empresa só dispuser de R$ 160.000,00, mas poderá tomar emprestado R$ 20.000,00, e pagar depois de um ano, sob a taxa de juros de 40%.
Solução:
A alternativa A continua com a mesma análise, enquanto que a B
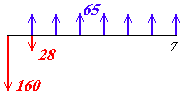
fica com duas saídas no seu fluxo de caixa, uma inicial de R$160.000,00 e outra, no primeiro ano de R$20.000,00(1,40) = R$28.000,00, que equivale a R$28.000/1,30 = R$21.538,46 também no início.
TIR(B) ==>
-160.000,00
-28.000,00/[1+i(B)]
+ 65.000,00
[P/A ; i(B)
; 7] = 0 ==>
TIR(B)
= 30,15 % a.a
TIR(B - A) ==>
-20.000,0020.000,00
-28.000,00/[1+i(B)] + 15.000,00
[P/A ; i
; 7] = 0 ==>
TIR(B
- A)
= 30,62 % a.a
3)
Qual destes investimentos (A ou B) é economicamente melhor para
uma empresa ?
(Considere
investimentos únicos, sem repetição
com TMA = 10% a.a)
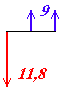
A) Investimento inicial de R$
11.800,00 e lucro líquido
anual de R$ 9.000,00,
durante 2
anos.
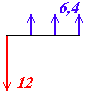
B) Investimento
inicial de R$
12.000,00 e lucro líquido
anual de R$ 6.400,00,
durante 3
anos.
Observação: E
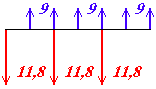
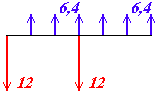
se a questão 3) fosse considerada como investimentos repetidos
?
Este método do Taxa Interna de Retorno (TIR) é equivalente aos outros:
-
Método do Valor Anual (VAUE)
-
Método da Valor Presente (VP)
KOPITTKE, H. Bruno e CASAROTTO FILHO, Nelson. Análise de Investimentos. São Paulo: Atlas, 2000.